Next: Newton's third law of Up: Newtonian mechanics Previous: Newton's first law of
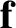 , then its equation of motion
is given by
where the momentum,
, then its equation of motion
is given by
where the momentum,  , is the product of the object's inertial
mass,
, is the product of the object's inertial
mass,  , and its velocity,
, and its velocity,  . If
. If  is not a function of time then Equation (2.13) reduces to the
familiar equation
Note that this equation is only valid in a inertial frame.
Clearly, the inertial mass of an object measures its reluctance to deviate
from its preferred state of uniform motion in a straight line (in an
inertial frame). Of course, the preceding equation of motion can only be solved if we have an independent expression for the force,
is not a function of time then Equation (2.13) reduces to the
familiar equation
Note that this equation is only valid in a inertial frame.
Clearly, the inertial mass of an object measures its reluctance to deviate
from its preferred state of uniform motion in a straight line (in an
inertial frame). Of course, the preceding equation of motion can only be solved if we have an independent expression for the force, 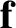 (i.e., a law of force).
Let us suppose that this is the case.
(i.e., a law of force).
Let us suppose that this is the case.
An important corollary of Newton's second law is that force is a vector
quantity. This must be the case, because the law equates force to the
product of a scalar (mass) and a vector (acceleration).2.2
Note that acceleration is obviously a vector because it is directly related to displacement, which is the prototype of all vectors. One consequence of force being a vector is
that two forces, 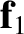 and
and  , both acting at a given
point, have the same effect as a single force,
, both acting at a given
point, have the same effect as a single force,
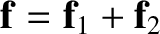 ,
acting at the same point, where the summation is performed according to the
laws of vector addition. Likewise, a single force,
,
acting at the same point, where the summation is performed according to the
laws of vector addition. Likewise, a single force, 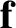 , acting at
a given point, has the same effect as two forces,
, acting at
a given point, has the same effect as two forces, 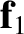 and
and  ,
acting at the same point, provided that
,
acting at the same point, provided that
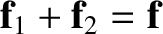 . This
method of combining and splitting forces is known as the resolution of
forces; it lies at the heart of many calculations in Newtonian mechanics.
. This
method of combining and splitting forces is known as the resolution of
forces; it lies at the heart of many calculations in Newtonian mechanics.
Taking the scalar product of Equation (2.14) with the velocity,  ,
we obtain
,
we obtain
 |
(2.15) |
 |
(2.17) |
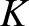 represents the energy that the object possesses by virtue of its motion.
This type of energy is generally known as kinetic energy. Thus, Equation (2.16) states that any work done on point object by an external force
goes to increase the object's kinetic energy.
represents the energy that the object possesses by virtue of its motion.
This type of energy is generally known as kinetic energy. Thus, Equation (2.16) states that any work done on point object by an external force
goes to increase the object's kinetic energy.
Suppose that, under the action of the force, 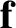 , our object moves
from point
, our object moves
from point 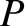 at time
at time  to point
to point 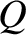 at time
at time 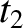 . The
net change in the object's kinetic energy is obtained by integrating
Equation (2.16):
. The
net change in the object's kinetic energy is obtained by integrating
Equation (2.16):
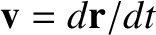 .
Here,
.
Here, 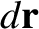 is an element of the object's path between points
is an element of the object's path between points 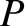 and
and 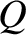 , and the integral in
, and the integral in 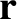 represents the net work done by the
force as the object moves along the path from
represents the net work done by the
force as the object moves along the path from 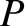 to
to 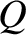 .
.
As is well known, there are basically two kinds
of forces in nature: first, those for which line integrals of the type
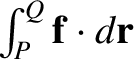 depend on the end points, but not
on the path taken between these points; second, those for which
line integrals of the type
depend on the end points, but not
on the path taken between these points; second, those for which
line integrals of the type
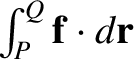 depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It can be
demonstrated that if the line integral
depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It can be
demonstrated that if the line integral
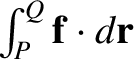 is path-independent, for all
choices of
is path-independent, for all
choices of  and
and  , then the force
, then the force 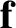 can
be written as the gradient of a scalar field. (See Section A.5.) In other words, all
conservative forces satisfy
can
be written as the gradient of a scalar field. (See Section A.5.) In other words, all
conservative forces satisfy
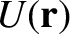 . [Incidentally, mathematicians, as opposed to physicists and astronomers, usually
write
. [Incidentally, mathematicians, as opposed to physicists and astronomers, usually
write
 .]
Note that
.]
Note that
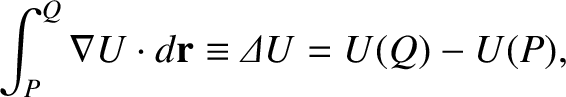 |
(2.20) |
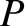 and
and 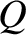 .
Hence, it follows from Equation (2.18)
that
.
Hence, it follows from Equation (2.18)
that
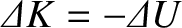 |
(2.21) |
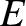 is the object's total energy, which is conserved;
is the object's total energy, which is conserved; 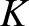 is the energy the
object has by virtue of its motion, otherwise known as its
kinetic energy; and
is the energy the
object has by virtue of its motion, otherwise known as its
kinetic energy; and 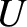 is the energy the object has by
virtue of its position, otherwise known as its potential
energy. Note, however, that we can write energy conservation
equations only for conservative forces. Gravity is an obvious example of such a force.
Incidentally, potential energy is undefined to an arbitrary additive constant.
In fact, it is only the difference in potential energy between
different points in space that is well defined.
is the energy the object has by
virtue of its position, otherwise known as its potential
energy. Note, however, that we can write energy conservation
equations only for conservative forces. Gravity is an obvious example of such a force.
Incidentally, potential energy is undefined to an arbitrary additive constant.
In fact, it is only the difference in potential energy between
different points in space that is well defined.