Let (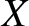 ,
, 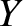 ,
, 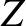 ) be Cartesian coordinates in the standard reference frame described in Section 4.12.
The relationship between the (
) be Cartesian coordinates in the standard reference frame described in Section 4.12.
The relationship between the (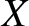 ,
, 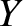 ,
, 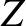 ) and the (
) and the ( ,
,  ,
,  ) coordinate systems is
) coordinate systems is
![\begin{displaymath}{\small\left(\!\!\begin{array}{c} X\\ [0.5ex]Y\\ [0.5ex]Z\end...
...egin{array}{c} x\\ [0.5ex]y\\ [0.5ex]z\end{array}\!\!\right). }\end{displaymath}](img5121.png) |
(I.33) |
Here, 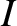 ,
,
 , and
, and  are the planet's orbital inclination to the ecliptic plane,
longitude of the ascending node (relative to the vernal equinox), and argument of the perihelion, respectively.
are the planet's orbital inclination to the ecliptic plane,
longitude of the ascending node (relative to the vernal equinox), and argument of the perihelion, respectively.
Equations (I.6) and (I.33) imply that
It follows that
However, Equations (I.19)–(I.21) can be combined with Equation (I.33) to give
Thus, Equations (I.22), (I.39), and (I.42) yield
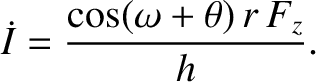 |
(I.43) |
Equations (I.34), (I.35), (I.37), and (I.38) imply that
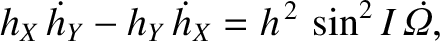 |
(I.44) |
or
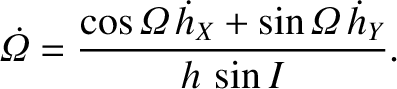 |
(I.45) |
However, it follows from Equations (I.40) and (I.41) that
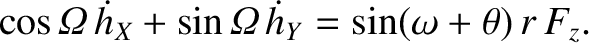 |
(I.46) |
Hence, we obtain
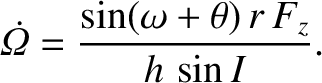 |
(I.47) |
According to Equations (I.8) and (I.33),
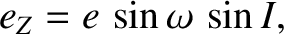 |
(I.48) |
which implies that
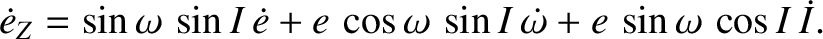 |
(I.49) |
Thus, it follows from Equations (I.27) and (I.43) that
However, Equations (I.24)–(I.26) and (I.33) give
A comparison of the previous two equations yields
![$\displaystyle \skew{3}\dot{\omega} = -\frac{h}{\mu}\,\frac{1}{e}\left[\cos\thet...
...theta\,F_\theta \right] -\frac{\cos I\,\sin(\omega+\theta)\,r\,F_z}{h\,\sin I}.$](img5150.png) |
(I.52) |
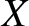 ,
, 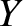 ,
, 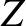 ) be Cartesian coordinates in the standard reference frame described in Section 4.12.
The relationship between the (
) be Cartesian coordinates in the standard reference frame described in Section 4.12.
The relationship between the (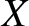 ,
, 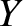 ,
, 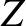 ) and the (
) and the ( ,
,  ,
,  ) coordinate systems is
Here,
) coordinate systems is
Here, 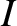 ,
,
 , and
, and  are the planet's orbital inclination to the ecliptic plane,
longitude of the ascending node (relative to the vernal equinox), and argument of the perihelion, respectively.
are the planet's orbital inclination to the ecliptic plane,
longitude of the ascending node (relative to the vernal equinox), and argument of the perihelion, respectively.
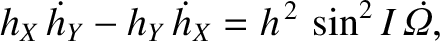
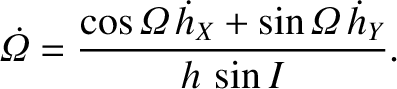
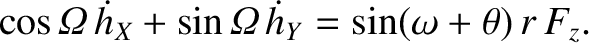
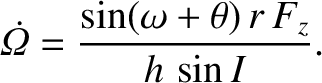
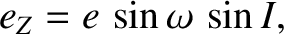
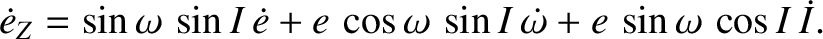
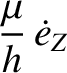
![$\displaystyle =\sin\omega\,\sin I\left[\sin\theta\,F_r+(\cos\theta+\cos E)\,F_\theta\right]
+ \frac{\mu}{h}\,e\,\cos\omega\,\sin I\,\skew{5}\dot{\omega}$](img5145.png)
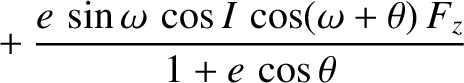
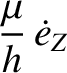
![$\displaystyle =\sin\omega\,\sin I\left[\sin\theta\,F_r+(\cos\theta+\cos E)\,F_\theta\right]$](img5147.png)
![$\displaystyle \phantom{=}-\cos\omega\,\sin I\left[\cos\theta\,F_r-\left(\frac{2+e\,\cos\theta}{1+e\,\cos\theta}\right)\sin\theta\,F_\theta \right]$](img5148.png)
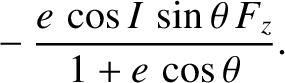
![$\displaystyle \skew{3}\dot{\omega} = -\frac{h}{\mu}\,\frac{1}{e}\left[\cos\thet...
...theta\,F_\theta \right] -\frac{\cos I\,\sin(\omega+\theta)\,r\,F_z}{h\,\sin I}.$](img5150.png)