Next: Expansion of orbital evolution Up: Derivation of Lagrange planetary Previous: Lagrange planetary equations
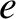 , and small inclination,
, and small inclination, 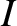 ,
certain terms on the right-hand sides of the Lagrange planetary equations become
singular. This problem
can be alleviated by defining the alternative orbital elements,
If we write the Lagrange planetary equations in terms of these new elements then we obtain
Note that the new equations now contain no singular terms in the limit
,
certain terms on the right-hand sides of the Lagrange planetary equations become
singular. This problem
can be alleviated by defining the alternative orbital elements,
If we write the Lagrange planetary equations in terms of these new elements then we obtain
Note that the new equations now contain no singular terms in the limit
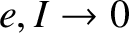 .
.
It is sometimes convenient to write the Lagrange planetary equations in terms of the mean anomaly,
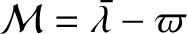 , and the argument of the perigee,
, and the argument of the perigee,
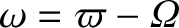 , rather than
, rather than
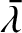 and
and
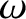 . Making the appropriate substitutions, the equations take the form (Brouwer and Clemence 1961)
. Making the appropriate substitutions, the equations take the form (Brouwer and Clemence 1961)
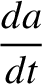 |
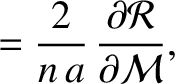 |
(G.131) |
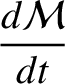 |
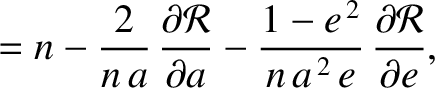 |
(G.132) |
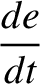 |
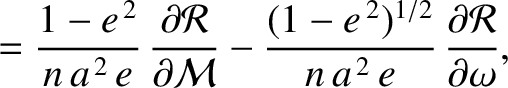 |
(G.133) |
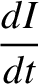 |
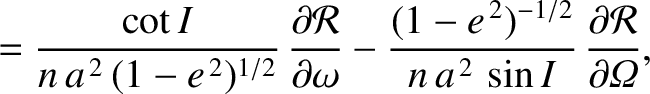 |
(G.134) |
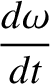 |
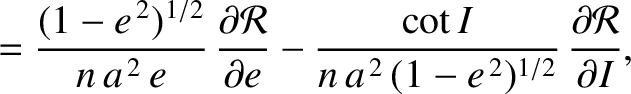 |
(G.135) |
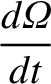 |
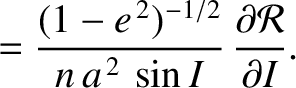 |
(G.136) |