Next: Lagrange brackets Up: Derivation of Lagrange planetary Previous: Introduction
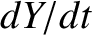 and
and 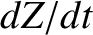 ,
were differentiated with respect to time, and the results substituted into Equations (G.3)–(G.5), then we would obtain three time evolution
equations for the six variables
,
were differentiated with respect to time, and the results substituted into Equations (G.3)–(G.5), then we would obtain three time evolution
equations for the six variables
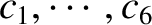 . In order to make
the problem definite, three additional conditions must be introduced into the problem.
It is convenient to choose
for
. In order to make
the problem definite, three additional conditions must be introduced into the problem.
It is convenient to choose
for 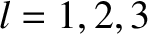 . Hence, it follows from Equations (G.12) and (G.13) that
. Hence, it follows from Equations (G.12) and (G.13) that
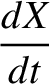 |
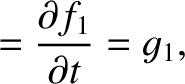 |
(G.15) |
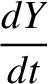 |
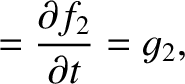 |
(G.16) |
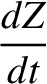 |
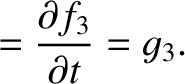 |
(G.17) |
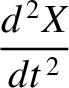 |
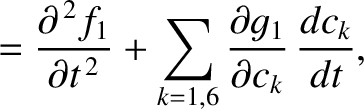 |
(G.18) |
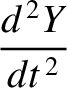 |
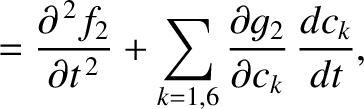 |
(G.19) |
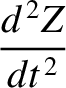 |
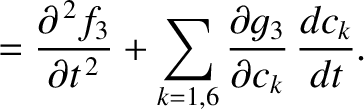 |
(G.20) |
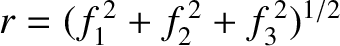 . Because
. Because 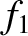 ,
, 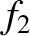 , and
, and 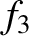 are the respective solutions to Equation (G.3)–(G.5) when the right-hand sides are
zero, and the orbital elements are thus constants, it follows that the
first two terms in each of the preceding three equations cancel one another. Hence,
writing
are the respective solutions to Equation (G.3)–(G.5) when the right-hand sides are
zero, and the orbital elements are thus constants, it follows that the
first two terms in each of the preceding three equations cancel one another. Hence,
writing 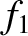 as
as 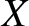 , and
, and 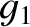 as
as 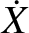 , and so on, Equations (G.14)
and (G.21)–(G.23) yield
These six equations are equivalent to the three original equations of motion
[(G.3)–(G.5)].
, and so on, Equations (G.14)
and (G.21)–(G.23) yield
These six equations are equivalent to the three original equations of motion
[(G.3)–(G.5)].