It is convenient to evaluate the disturbing function,
 |
(B.23) |
in a frame of reference that is instantaneously aligned with the ecliptic plane, as described in Section 4.12.
Let ( ,
,  ,
,  ) and (
) and (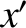 ,
, 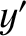 ,
, 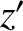 ) be the Cartesian components of
) be the Cartesian components of 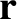 and
and 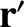 , respectively, in this
standard reference frame. It follows from Equations (4.38), and (4.72)–(4.74), that
as well as
where
Here,
, respectively, in this
standard reference frame. It follows from Equations (4.38), and (4.72)–(4.74), that
as well as
where
Here,  ,
,  ,
,  ,
,  ,
, 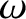 , and
, and
 are the orbital true anomaly, major radius, eccentricity, inclination, argument of the perihelion, and
longitude of the ascending node, respectively, of Mercury. Moreover,
are the orbital true anomaly, major radius, eccentricity, inclination, argument of the perihelion, and
longitude of the ascending node, respectively, of Mercury. Moreover, 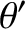 ,
,  ,
, 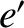 ,
, 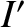 ,
, 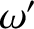 , and
, and
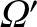 are the
corresponding quantities for the perturbing planet.
are the
corresponding quantities for the perturbing planet.
It is helpful to define
Making use of Equations (B.25)–(B.30), we deduce that
and
Hence,
![$\displaystyle {\cal R}(r,\theta) = \mu'\left[\frac{1}{(r^{\,2} + r'^{\,2}-2\,r\,r'\,\beta)^{1/2}}-\frac{\beta\,r}{r'^{\,2}}\right],$](img4188.png) |
(B.36) |
which implies that
![$\displaystyle \frac{\partial{\cal R}}{\partial r} =- \mu'\,r'\left[\frac{r/r'-\beta}{(r^{\,2} + r'^{\,2}-2\,r\,r'\,\beta)^{3/2}} + \frac{\beta}{r'^{\,3}}\right],$](img4189.png) |
(B.37) |
and
![$\displaystyle \frac{1}{r}\,\frac{\partial{\cal R}}{\partial\theta} = \mu'\,r'\,...
...rac{1}{(r^{\,2} + r'^{\,2}-2\,r\,r'\,\beta)^{3/2}} - \frac{1}{r'^{\,3}}\right],$](img4190.png) |
(B.38) |

 ,
,  ,
,  ) and (
) and (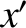 ,
, 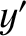 ,
, 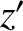 ) be the Cartesian components of
) be the Cartesian components of 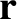 and
and 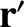 , respectively, in this
standard reference frame. It follows from Equations (4.38), and (4.72)–(4.74), that
, respectively, in this
standard reference frame. It follows from Equations (4.38), and (4.72)–(4.74), that

![$\displaystyle = r\,\left[\cos{\mit\Omega}\,\cos(\omega+\theta) - \sin{\mit\Omega}\,\sin(\omega+\theta)\,\cos I\right],$](img745.png)
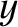
![$\displaystyle = r\,\left[ \sin{\mit\Omega}\,\cos(\omega+\theta) +\cos{\mit\Omega}\,\sin(\omega+\theta)\,\cos I\right],$](img747.png)
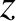


![$\displaystyle = r'\,\left[\cos{\mit\Omega}'\,\cos(\omega'+\theta') - \sin{\mit\Omega}'\,\sin(\omega'+\theta')\,\cos I'\right],$](img4166.png)
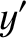
![$\displaystyle = r'\,\left[ \sin{\mit\Omega}'\,\cos(\omega'+\theta') +\cos{\mit\Omega}'\,\sin(\omega'+\theta')\,\cos I'\right],$](img4167.png)
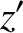
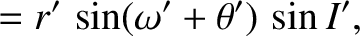
 ,
,  ,
,  ,
,  ,
, 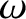 , and
, and
 are the orbital true anomaly, major radius, eccentricity, inclination, argument of the perihelion, and
longitude of the ascending node, respectively, of Mercury. Moreover,
are the orbital true anomaly, major radius, eccentricity, inclination, argument of the perihelion, and
longitude of the ascending node, respectively, of Mercury. Moreover, 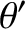 ,
,  ,
, 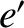 ,
, 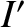 ,
, 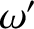 , and
, and
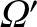 are the
corresponding quantities for the perturbing planet.
are the
corresponding quantities for the perturbing planet.

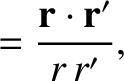
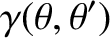
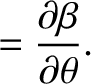
![$\displaystyle {\cal R}(r,\theta) = \mu'\left[\frac{1}{(r^{\,2} + r'^{\,2}-2\,r\,r'\,\beta)^{1/2}}-\frac{\beta\,r}{r'^{\,2}}\right],$](img4188.png)