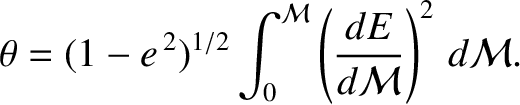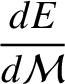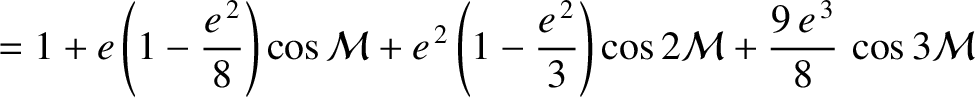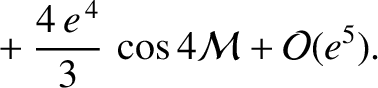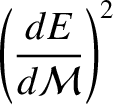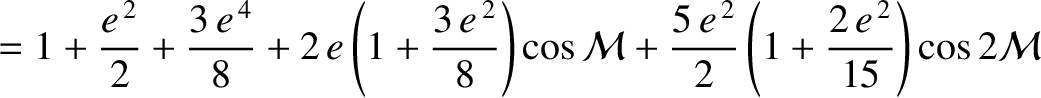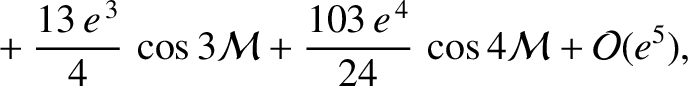Elliptic expansions
The well-known Bessel functions of the first kind,  , where
, where  is an integer, are defined as the
Fourier coefficients in the expansion of
is an integer, are defined as the
Fourier coefficients in the expansion of
 :
:
 |
(A.116) |
It follows that
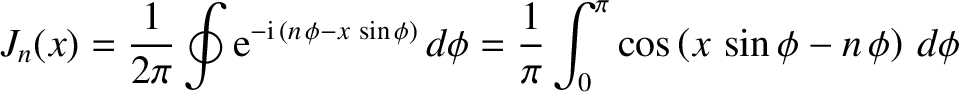 |
(A.117) |
(Gradshteyn and Ryzhik 1980a).
The Taylor expansion of  about
about 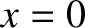 is
is
 |
(A.118) |
for 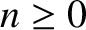 (Gradshteyn and Ryzhik 1980b). Moreover,
In particular,
(Gradshteyn and Ryzhik 1980b). Moreover,
In particular,
Let us write
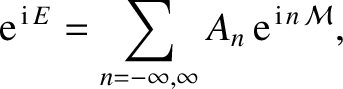 |
(A.125) |
where 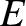 is the eccentric anomaly, and
is the eccentric anomaly, and 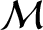 the mean anomaly, of
a Keplerian elliptic orbit. (See Section 4.11.)
It follows that
the mean anomaly, of
a Keplerian elliptic orbit. (See Section 4.11.)
It follows that
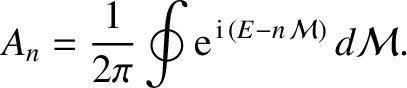 |
(A.126) |
Integrating by parts, we obtain
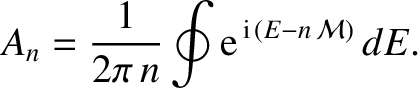 |
(A.127) |
However, according to Equation (4.59), the relationship between the eccentric and the mean anomalies is
 |
(A.128) |
where  is the orbital eccentricity. Hence,
is the orbital eccentricity. Hence,
![$\displaystyle A_n = \frac{1}{2\pi\,n} \oint {\rm e}^{-{\rm i}\,[(n-1)\,E - n\,e\,\sin E]}\,dE.$](img4044.png) |
(A.129) |
Comparison with Equation (A.117) reveals that
 |
(A.130) |
For the special case 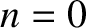 , L'Hopital's rule, together with Equations (A.119) and (A.122), yields
, L'Hopital's rule, together with Equations (A.119) and (A.122), yields
 |
(A.131) |
where  denotes a derivative.
denotes a derivative.
The real part of Equation (A.125) gives
where use has been made of Equations (A.120), (A.130), and (A.131). Likewise, the
imaginary part of Equation (A.125) yields
![$\displaystyle \sin E = \sum_{n=1,\infty}\left[\frac{J_{n-1}(n\,e)+ J_{n+1}(n\,e)}{n}\right]\sin(n\,{\cal M}).$](img4051.png) |
(A.133) |
It follows from Equations (A.121)–(A.124) that
Hence, from Equation (A.128),
According to Equation (4.69),
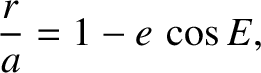 |
(A.137) |
where 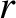 is is the radial distance from the focus of the orbit and
is is the radial distance from the focus of the orbit and  is the orbital major radius. Thus,
is the orbital major radius. Thus,
Equations (4.39) and (4.67) imply that
 |
(A.139) |
where  is the true anomaly. Hence, it follows from Equations (A.128) and (A.137), and the
fact that
is the true anomaly. Hence, it follows from Equations (A.128) and (A.137), and the
fact that 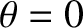 when
when
 , that
, that
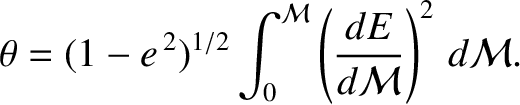 |
(A.140) |
From Equation (A.136),
Thus,
and
 , where
, where  is an integer, are defined as the
Fourier coefficients in the expansion of
is an integer, are defined as the
Fourier coefficients in the expansion of
 :
:

 about
about 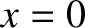 is
is

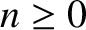 (Gradshteyn and Ryzhik 1980b). Moreover,
In particular,
(Gradshteyn and Ryzhik 1980b). Moreover,
In particular,
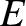 is the eccentric anomaly, and
is the eccentric anomaly, and  the mean anomaly, of
a Keplerian elliptic orbit. (See Section 4.11.)
It follows that
the mean anomaly, of
a Keplerian elliptic orbit. (See Section 4.11.)
It follows that
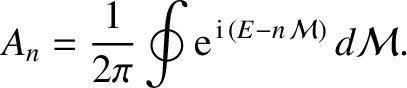
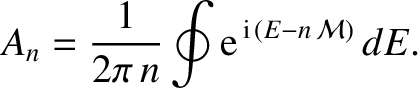
 is the orbital eccentricity. Hence,
is the orbital eccentricity. Hence,
![$\displaystyle A_n = \frac{1}{2\pi\,n} \oint {\rm e}^{-{\rm i}\,[(n-1)\,E - n\,e\,\sin E]}\,dE.$](img4044.png)
 , L'Hopital's rule, together with Equations (A.119) and (A.122), yields
where
, L'Hopital's rule, together with Equations (A.119) and (A.122), yields
where  denotes a derivative.
denotes a derivative.
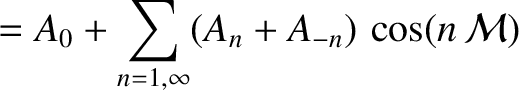
![$\displaystyle =-\frac{e}{2} + \sum_{n=1,\infty}
\left[\frac{J_{n-1}(n\,e)-J_{-n-1}(-n\,e)}{n}\right]\cos (n\,{\cal M})$](img4049.png)
![$\displaystyle = -\frac{e}{2} + \sum_{n=1,\infty}\left[\frac{J_{n-1}(n\,e)-J_{n+1}(n\,e)}{n}\right]\cos(n\,{\cal M}),$](img4050.png)
![$\displaystyle \sin E = \sum_{n=1,\infty}\left[\frac{J_{n-1}(n\,e)+ J_{n+1}(n\,e)}{n}\right]\sin(n\,{\cal M}).$](img4051.png)
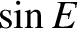
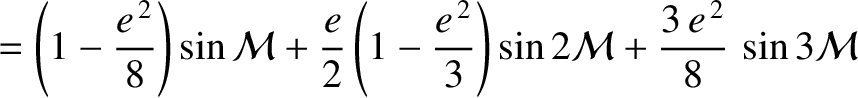
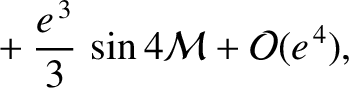
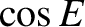
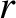 is is the radial distance from the focus of the orbit and
is is the radial distance from the focus of the orbit and  is the orbital major radius. Thus,
is the orbital major radius. Thus,

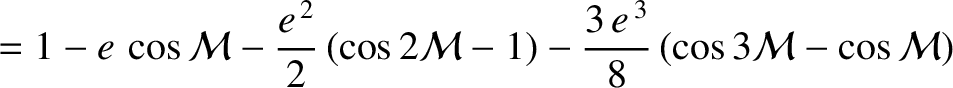
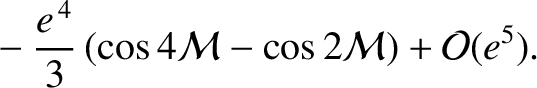

 is the true anomaly. Hence, it follows from Equations (A.128) and (A.137), and the
fact that
is the true anomaly. Hence, it follows from Equations (A.128) and (A.137), and the
fact that 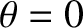 when
when
 , that
, that