Next: Lagrangian mechanics Up: Rotating reference frames Previous: Roche radius
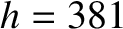 m, latitude
m, latitude 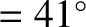 N). Find the ball bearing's horizontal deflection (magnitude and direction)
at the bottom of the shaft due to the Coriolis force . Neglect air resistance. (Modified from Fowles and Cassiday 2005.)
N). Find the ball bearing's horizontal deflection (magnitude and direction)
at the bottom of the shaft due to the Coriolis force . Neglect air resistance. (Modified from Fowles and Cassiday 2005.)
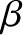 , from a point
on the Earth's surface whose latitude is
, from a point
on the Earth's surface whose latitude is 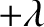 . Demonstrate that the projectile strikes the
ground with a lateral deflection
. Demonstrate that the projectile strikes the
ground with a lateral deflection
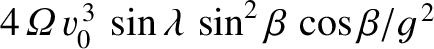 .
Is the deflection northward or southward?
Here,
.
Is the deflection northward or southward?
Here,
 is the Earth's angular velocity,
is the Earth's angular velocity,  the projectile's initial speed, and
the projectile's initial speed, and
 the acceleration due to gravity. Neglect air resistance. (Modified from Thornton and Marion 2004.)
the acceleration due to gravity. Neglect air resistance. (Modified from Thornton and Marion 2004.)
 rolls without friction over a horizontal plane located on the surface of the Earth.
Show that in the northern hemisphere it rolls in a clockwise sense (seen from above) around
a circle of radius
rolls without friction over a horizontal plane located on the surface of the Earth.
Show that in the northern hemisphere it rolls in a clockwise sense (seen from above) around
a circle of radius
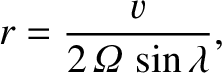
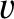 is the speed of the ball,
is the speed of the ball,
 the Earth's angular velocity, and
the Earth's angular velocity, and 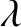 the
terrestrial latitude.
the
terrestrial latitude.
 about the Earth.
Let us define a set of co-moving Cartesian coordinates, centered on the satellite, such that
the
about the Earth.
Let us define a set of co-moving Cartesian coordinates, centered on the satellite, such that
the  -axis always points toward the center of the Earth, the
-axis always points toward the center of the Earth, the  -axis in the
direction of the satellite's orbital motion, and the
-axis in the
direction of the satellite's orbital motion, and the  -axis in the direction
of the satellite's orbital angular velocity,
-axis in the direction
of the satellite's orbital angular velocity,
 . Demonstrate that the
equation of motion of a small mass in orbit about the satellite are
. Demonstrate that the
equation of motion of a small mass in orbit about the satellite are
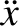 |
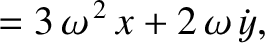 |
|
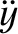 |
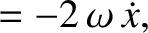 |
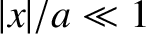 and
and
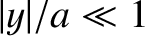 . Neglect the gravitational
attraction between the satellite and the mass.
Show that the mass
executes a retrograde (i.e., in the opposite sense to the
satellite's orbital rotation) elliptical orbit about the satellite whose
period matches that of the satellite's orbit, and whose major and minor axes
are in the ratio
. Neglect the gravitational
attraction between the satellite and the mass.
Show that the mass
executes a retrograde (i.e., in the opposite sense to the
satellite's orbital rotation) elliptical orbit about the satellite whose
period matches that of the satellite's orbit, and whose major and minor axes
are in the ratio 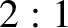 , and are aligned along the
, and are aligned along the  - and
- and  -axes,
respectively.
-axes,
respectively.
 , with terrestrial latitude,
, with terrestrial latitude, 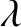 , is
, is
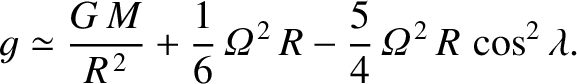
 is the terrestrial mass,
is the terrestrial mass,  the mean terrestrial radius, and
the mean terrestrial radius, and
 the terrestrial axial
angular velocity.
the terrestrial axial
angular velocity.
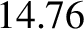 days.
days.
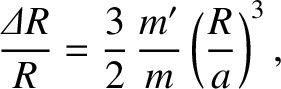
 is the mass of the Earth,
is the mass of the Earth, 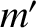 the mass of the Moon,
the mass of the Moon,  the radius of the Earth, and
the radius of the Earth, and  the
radius of the lunar orbit. Show that
the
radius of the lunar orbit. Show that
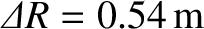 , and also that the tidal elongation of the ocean
layer due to the Sun is such that
, and also that the tidal elongation of the ocean
layer due to the Sun is such that
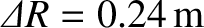 .
.
 , radius
, radius  , and effective rigidity
, and effective rigidity
 , is in a circular orbit of major radius
, is in a circular orbit of major radius  about a
spherical planet of mass
about a
spherical planet of mass 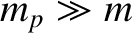 . The moon rotates about an axis passing through its center of mass
that is directed normal to the orbital plane. Suppose that the moon is in a synchronous state such that its
rotational angular velocity,
. The moon rotates about an axis passing through its center of mass
that is directed normal to the orbital plane. Suppose that the moon is in a synchronous state such that its
rotational angular velocity,
 , matches its orbital angular velocity,
, matches its orbital angular velocity,
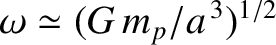 .
Let
.
Let  ,
,  ,
,  be a set of Cartesian coordinates, centered on the moon, such that the
be a set of Cartesian coordinates, centered on the moon, such that the  -axis is normal to
the orbital plane, and the
-axis is normal to
the orbital plane, and the  -axis is directed from the center of the moon to the center of the planet. Assuming that
the moon responds elastically to the centrifugal and tidal potentials, show that the
changes in radius, parallel to the three coordinate axes, induced by the centrifugal potential are
-axis is directed from the center of the moon to the center of the planet. Assuming that
the moon responds elastically to the centrifugal and tidal potentials, show that the
changes in radius, parallel to the three coordinate axes, induced by the centrifugal potential are
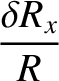 |
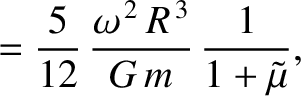 |
|
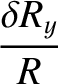 |
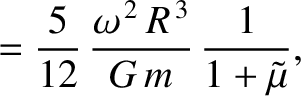 |
|
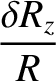 |
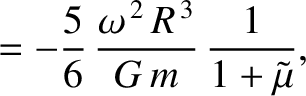 |
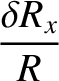 |
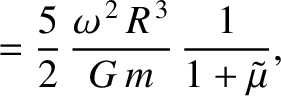 |
|
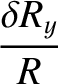 |
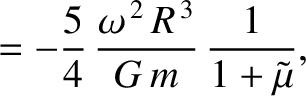 |
|
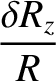 |
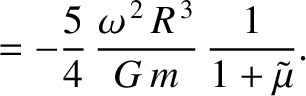 |
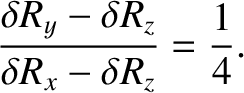 |
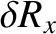 ,
,
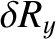 , and
, and
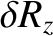 for the Earth's Moon (which is in a synchronous state).
for the Earth's Moon (which is in a synchronous state).
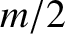 connected by a light rigid rod of length
connected by a light rigid rod of length 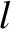 . The
satellite is placed in a circular orbit of radius
. The
satellite is placed in a circular orbit of radius 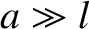 (measured from the mid-point of the rod) around a planet of mass
(measured from the mid-point of the rod) around a planet of mass 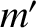 . The
rod is oriented such that
it always points toward the center of the planet. Demonstrate that the tension in the rod is
. The
rod is oriented such that
it always points toward the center of the planet. Demonstrate that the tension in the rod is