Next: Newton's second law of Up: Newtonian mechanics Previous: Newton's laws of motion
Suppose that we have found an inertial frame of reference. Let us
set up a Cartesian coordinate system in this frame. The motion
of a point object can now be specified by giving its position vector,
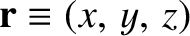 ,
with respect to the origin of the coordinate system, as a function of time,
,
with respect to the origin of the coordinate system, as a function of time, 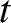 .
Consider a second frame of reference moving with some
constant velocity
.
Consider a second frame of reference moving with some
constant velocity
 with respect to the first frame. Without loss of generality,
we can suppose that the Cartesian axes in the second frame are parallel
to the corresponding axes in the first frame, that
with respect to the first frame. Without loss of generality,
we can suppose that the Cartesian axes in the second frame are parallel
to the corresponding axes in the first frame, that
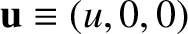 ,
and, finally, that the origins of the two frames instantaneously coincide at
,
and, finally, that the origins of the two frames instantaneously coincide at 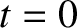 . See Figure 2.1. Suppose that the position vector
of our point object is
. See Figure 2.1. Suppose that the position vector
of our point object is
 in the second frame of reference.
It is evident, from Figure 2.1, that at any given time,
in the second frame of reference.
It is evident, from Figure 2.1, that at any given time, 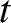 , the coordinates of the
object in the two reference frames satisfy
, the coordinates of the
object in the two reference frames satisfy
By definition, the instantaneous velocity of the object in our first reference frame is given by
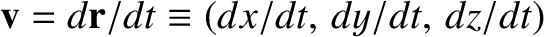 , with an analogous
expression for the velocity,
, with an analogous
expression for the velocity, 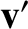 , in the second frame.
It follows, from differentiation of Equations (2.1)–(2.3) with respect to time, that the velocity components in the two frames satisfy
, in the second frame.
It follows, from differentiation of Equations (2.1)–(2.3) with respect to time, that the velocity components in the two frames satisfy
Finally, by definition, the instantaneous acceleration of the object in our first reference frame is given by
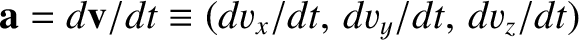 , with an analogous
expression for the acceleration,
, with an analogous
expression for the acceleration, 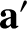 , in the second frame.
It follows, from differentiation of Equations (2.4)–(2.6) with respect to time, that the acceleration
components in the two frames satisfy
, in the second frame.
It follows, from differentiation of Equations (2.4)–(2.6) with respect to time, that the acceleration
components in the two frames satisfy
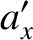 |
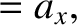 |
(2.8) |
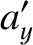 |
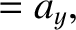 |
(2.9) |
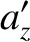 |
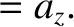 |
(2.10) |
According to Equations (2.7) and (2.11), if an
object moves in a straight line with a constant speed in our original
inertial frame (i.e., if
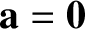 ) then it also
moves in a (different) straight line with a (different) constant speed
in the second frame of reference (i.e.,
) then it also
moves in a (different) straight line with a (different) constant speed
in the second frame of reference (i.e.,
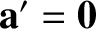 ). Hence,
we conclude that the second frame of reference is also an inertial frame.
). Hence,
we conclude that the second frame of reference is also an inertial frame.
A simple extension of the preceding argument allows us to conclude that there exists an infinite number of different inertial frames moving with constant velocities with respect to one another. Newton thought that one of these inertial frames was special and defined an absolute standard of rest; that is, a static object in this frame was in a state of absolute rest. However, Einstein showed that this is not the case. In fact, there is no absolute standard of rest, which implies that all motion is relative—hence, the name “relativity” for Einstein's theory. Consequently, one inertial frame is just as good as another as far as Newtonian mechanics is concerned.
But what happens if the second frame of reference accelerates with respect to the first? In this case, it is not hard to see that Equation (2.11) generalizes to
where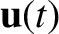 is the instantaneous velocity of the second frame
with respect to the first. According to this formula, if an object
moves in a straight line with a constant speed in the first frame (i.e., if
is the instantaneous velocity of the second frame
with respect to the first. According to this formula, if an object
moves in a straight line with a constant speed in the first frame (i.e., if
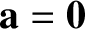 ) then it does not move in a
straight line with a constant speed
in the second frame (i.e.,
) then it does not move in a
straight line with a constant speed
in the second frame (i.e.,
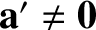 ). Hence,
if the first frame is an inertial frame then the second is not.
). Hence,
if the first frame is an inertial frame then the second is not.
A simple extension of the preceding argument allows us to conclude that any frame of reference that accelerates with respect to a given inertial frame is not itself an inertial frame.
For most practical purposes, when studying the motions of objects close to the
Earth's surface, a reference frame that is fixed with
respect to this surface is approximately inertial. However,
if the trajectory of a projectile within such a frame is measured to high
precision then it will be found to deviate slightly from the predictions
of Newtonian mechanics. (See Chapter 6.) This deviation
is due to the fact that the Earth is rotating about a north-south axis, and its surface is therefore
accelerating towards this axis (the residual acceleration is about
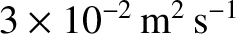 ). When studying the orbits of
objects around the Earth, a reference frame whose origin
is the center of the Earth (or, to be more exact, the center of mass of the Earth-Moon system), and whose coordinate axes are fixed with respect
to distant stars, is approximately inertial. However, if such
orbits are measured to extremely high precision then they will
again be found to deviate very slightly from the predictions of Newtonian
mechanics. In this case, the deviation is due to the Earth's orbital
rotation about the Sun (the residual acceleration is about
). When studying the orbits of
objects around the Earth, a reference frame whose origin
is the center of the Earth (or, to be more exact, the center of mass of the Earth-Moon system), and whose coordinate axes are fixed with respect
to distant stars, is approximately inertial. However, if such
orbits are measured to extremely high precision then they will
again be found to deviate very slightly from the predictions of Newtonian
mechanics. In this case, the deviation is due to the Earth's orbital
rotation about the Sun (the residual acceleration is about
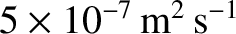 ). When studying the orbits of the planets
in the solar system, a reference frame whose origin is the center of the Sun (or, to be more exact, the center of mass of the
solar system), and whose coordinate axes are fixed with respect
to distant stars, is approximately inertial. In this case, any deviations
of the orbits from the predictions of Newtonian mechanics
due to the orbital rotation of the Sun about the galactic center are
extremely small (the residual acceleration is about
). When studying the orbits of the planets
in the solar system, a reference frame whose origin is the center of the Sun (or, to be more exact, the center of mass of the
solar system), and whose coordinate axes are fixed with respect
to distant stars, is approximately inertial. In this case, any deviations
of the orbits from the predictions of Newtonian mechanics
due to the orbital rotation of the Sun about the galactic center are
extremely small (the residual acceleration is about
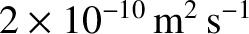 ). It should be noted that it is impossible
to identify an absolute inertial frame. The best approximation to such
a frame is the so-called International Celestial Reference System (ICRF), which is defined with respect to extremely distant point radio sources (mostly quasars) whose positions can be measured to great accuracy via very long baseline interferometry (VLBI) (Charlot 2020). However, for a given dynamical problem, it is always
possible to identify an approximate inertial frame.
However, for a given dynamical problem, it is always
possible to identify an approximate inertial frame. Furthermore, any
deviations of such a frame from a true inertial frame can be incorporated
into the framework of Newtonian mechanics via the introduction of so-called fictitious forces. (See Chapter 6.)
). It should be noted that it is impossible
to identify an absolute inertial frame. The best approximation to such
a frame is the so-called International Celestial Reference System (ICRF), which is defined with respect to extremely distant point radio sources (mostly quasars) whose positions can be measured to great accuracy via very long baseline interferometry (VLBI) (Charlot 2020). However, for a given dynamical problem, it is always
possible to identify an approximate inertial frame.
However, for a given dynamical problem, it is always
possible to identify an approximate inertial frame. Furthermore, any
deviations of such a frame from a true inertial frame can be incorporated
into the framework of Newtonian mechanics via the introduction of so-called fictitious forces. (See Chapter 6.)