Next: Keplerian orbits Up: Newtonian gravity Previous: Potential due to uniform
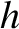 .
Show that if the variation of gravity with height is allowed for, but the
resistance of air is neglected, then the height reached will be greater by
.
Show that if the variation of gravity with height is allowed for, but the
resistance of air is neglected, then the height reached will be greater by
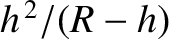 , where
, where
 is the Earth's radius. (From Lamb 1923.)
is the Earth's radius. (From Lamb 1923.)
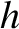 is
is
![$\displaystyle \frac{1}{3}\left(\frac{2\,R}{g}\right)^{1/2}\,\left[\left(1+\frac{h}{R}\right)^{3/2}-1\right],
$](img529.png)
 is the Earth's radius, and
is the Earth's radius, and  its surface gravitational acceleration. (From Lamb 1923.)
its surface gravitational acceleration. (From Lamb 1923.)
 , and neglecting air resistance, show that
a particle that starts from rest a distance
, and neglecting air resistance, show that
a particle that starts from rest a distance  from the Earth's surface will reach the surface with
speed
from the Earth's surface will reach the surface with
speed
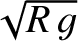 after a time
after a time
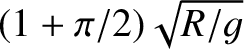 , where
, where  is the surface gravitational acceleration.
(Modified from Smart 1951.)
is the surface gravitational acceleration.
(Modified from Smart 1951.)
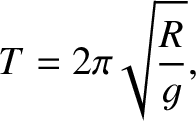
 is the radius of the sphere, and
is the radius of the sphere, and  the gravitational acceleration at its surface.
the gravitational acceleration at its surface.
 point objects interacting via
gravity.
The equation of motion of the
point objects interacting via
gravity.
The equation of motion of the  th object is
th object is
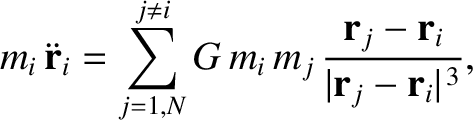
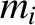 and
and 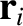 are the mass and position vector of this object, respectively.
Moreover, the total potential energy of the system takes the form
are the mass and position vector of this object, respectively.
Moreover, the total potential energy of the system takes the form
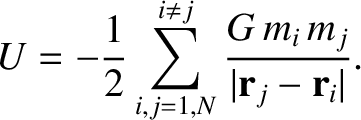
 . Demonstrate, from the equations of motion, that
. Demonstrate, from the equations of motion, that 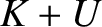 is constant in time.
is constant in time.
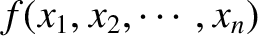 . Such a function that satisfies
. Such a function that satisfies
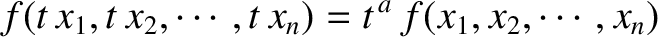
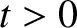 , and all values of the
, and all values of the 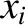 , is termed a homogeneous function of degree
, is termed a homogeneous function of degree  .
Prove the following theorem regarding homogeneous functions:
.
Prove the following theorem regarding homogeneous functions:
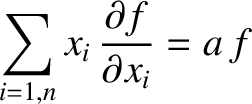
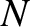 point particles interacting via
attractive central forces. Let the mass and position vector of the
point particles interacting via
attractive central forces. Let the mass and position vector of the  th particle be
th particle be
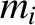 and
and 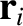 , respectively. Suppose that magnitude of the force exerted on particle
, respectively. Suppose that magnitude of the force exerted on particle  by
particle
by
particle 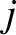 is
is
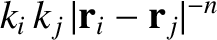 . Here,
. Here, 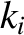 measures
some constant physical
property of the
measures
some constant physical
property of the  th particle (e.g., its electric charge).
Show that the total potential energy
th particle (e.g., its electric charge).
Show that the total potential energy 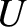 of the system is written
of the system is written
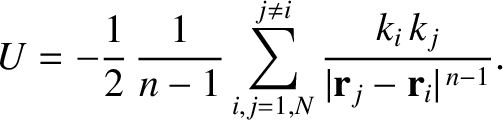
 th particle can be written
th particle can be written
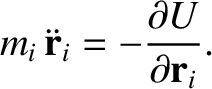
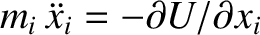 ,
,
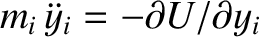 , etc., where the
, etc., where the 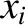 ,
, 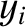 ,
, 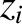 , for
, for 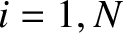 , are treated as independent variables.)
Use the mathematical
theorem from the previous exercise to show that
, are treated as independent variables.)
Use the mathematical
theorem from the previous exercise to show that
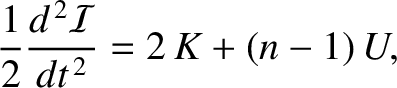
 , and
, and  is the total kinetic energy.
This result is known as the virial theorem.
Demonstrate that when
is the total kinetic energy.
This result is known as the virial theorem.
Demonstrate that when 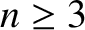 the system possesses no virial equilibria (i.e., states for which
the system possesses no virial equilibria (i.e., states for which
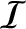 does not evolve in time) that are bounded.
does not evolve in time) that are bounded.
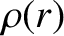 that extends out to
that extends out to 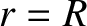 can be
written
can be
written

![$\displaystyle \rho(r) = \left\{\begin{array}{lcc} \rho_0\,r^{-\alpha}&\mbox{\hspace{1cm}}& r \leq R\\ [0.5ex]
0&& r>R\end{array}\right.,
$](img556.png)
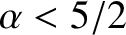 , then
, then

 is the total mass.
is the total mass.

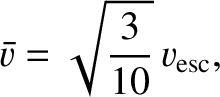
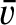 is the mean stellar velocity, and
is the mean stellar velocity, and
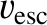 is the escape speed (i.e., the speed
a star at the edge of the cluster would require in order to escape to infinity.) See Section 3.8, Exercise 7.
is the escape speed (i.e., the speed
a star at the edge of the cluster would require in order to escape to infinity.) See Section 3.8, Exercise 7.
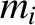 and
position vector
and
position vector 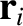 , interacting
via gravity. Show that, for such a system, the virial theorem implies that
, interacting
via gravity. Show that, for such a system, the virial theorem implies that
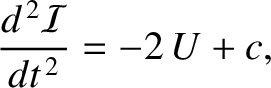
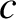 is a constant,
is a constant,
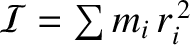 , and the
, and the 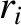 are measured from the geometric center. Hence, deduce that the angular frequency of
small-amplitude radial pulsations
of the star (in which the radial displacement is directly proportional to the radial distance from the center) takes the form
are measured from the geometric center. Hence, deduce that the angular frequency of
small-amplitude radial pulsations
of the star (in which the radial displacement is directly proportional to the radial distance from the center) takes the form
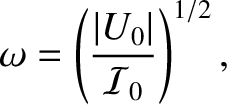
 and
and
 are the equilibrium values of
are the equilibrium values of 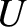 and
and 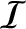 . Finally, show that if the mass
density within the star varies as
. Finally, show that if the mass
density within the star varies as
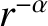 , where
, where  is the radial distance from the geometric center, and where
is the radial distance from the geometric center, and where
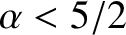 , then
, then
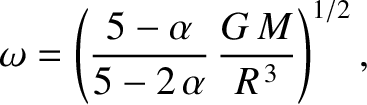
 and
and  are the stellar mass and radius, respectively. See Section 3.8, Exercises 7 and 8.
are the stellar mass and radius, respectively. See Section 3.8, Exercises 7 and 8.