Next: Axially symmetric mass distributions Up: Newtonian gravity Previous: Gravitational potential
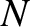 point masses
point masses 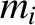 located at position vectors
located at position vectors
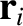 (where
(where  runs from 1 to
runs from 1 to 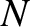 ).
What is the gravitational potential energy stored in such a collection? In other words, how much work would we have to do in order to assemble
the masses, starting from an initial state in which they are all
at rest and very widely
separated?
).
What is the gravitational potential energy stored in such a collection? In other words, how much work would we have to do in order to assemble
the masses, starting from an initial state in which they are all
at rest and very widely
separated?
We have seen that a gravitational acceleration field can be expressed in terms of a gravitational potential:
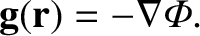 |
(3.11) |
 located at position
located at position  is
written
is
written
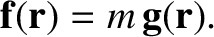 |
(3.12) |
 to point
to point  is simply
The negative sign in the preceding expression comes about because we would have to
exert a force
is simply
The negative sign in the preceding expression comes about because we would have to
exert a force 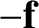 on the mass to counteract the force
exerted by the gravitational field. Recall, finally, that the gravitational potential
generated by a point mass
on the mass to counteract the force
exerted by the gravitational field. Recall, finally, that the gravitational potential
generated by a point mass 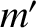 located at position
located at position 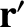 is
is
Let us build up our collection of masses one by one. It takes no work to bring the
first mass from infinity, because there is no gravitational field to fight against.
Let us clamp this mass in position at 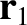 . In order to bring the
second mass into position at
. In order to bring the
second mass into position at 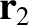 ,
we have to do work against the gravitational field
generated by the first mass. According to Equations (3.13) and (3.14),
this work is given by
,
we have to do work against the gravitational field
generated by the first mass. According to Equations (3.13) and (3.14),
this work is given by
 is simply the sum of the works done against the gravitational fields generated by
masses 1 and 2 taken in isolation:
is simply the sum of the works done against the gravitational fields generated by
masses 1 and 2 taken in isolation:
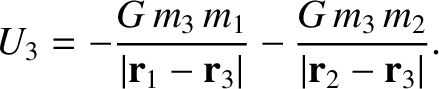 |
(3.16) |
 |
(3.17) |
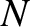 point masses, giving
point masses, giving
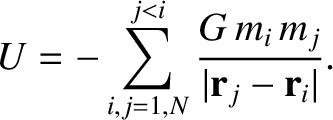 |
(3.18) |
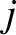 must be less than
must be less than  makes the preceding summation
rather messy. If we were to sum without restriction (other than
makes the preceding summation
rather messy. If we were to sum without restriction (other than 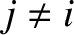 ) then
each pair of masses would be counted twice. It is convenient to do just
this, and then to divide the result by two. Thus, we obtain
This is the potential energy of an arrangement of point masses. We can think of this quantity as the
work required to bring the masses from infinity and assemble them in the
required formation. The fact that the work is negative implies that we would gain energy during this process.
) then
each pair of masses would be counted twice. It is convenient to do just
this, and then to divide the result by two. Thus, we obtain
This is the potential energy of an arrangement of point masses. We can think of this quantity as the
work required to bring the masses from infinity and assemble them in the
required formation. The fact that the work is negative implies that we would gain energy during this process.
Equation (3.19) can be written
where is the gravitational potential experienced by the th mass due to the other
masses in the distribution.
For the case of a continuous mass distribution, we can generalize the preceding result to give
where
is the familiar gravitational potential generated by a continuous mass distribution
of mass density
th mass due to the other
masses in the distribution.
For the case of a continuous mass distribution, we can generalize the preceding result to give
where
is the familiar gravitational potential generated by a continuous mass distribution
of mass density
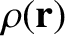 .
.