Next: Preliminary analysis Up: Derivation of Lagrange planetary Previous: Derivation of Lagrange planetary
 and relative position vector
and relative position vector  that is orbiting around the Sun, whose mass is
that is orbiting around the Sun, whose mass is  . The planet's equation of motion is written (see Section 4.16)
. The planet's equation of motion is written (see Section 4.16)
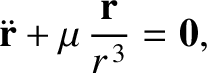 |
(G.1) |
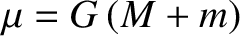 . As described in Chapter 4, the solution to this equation is
a Keplerian ellipse whose properties are fully determined after six integrals of the motion, known
as orbital elements, are specified.
. As described in Chapter 4, the solution to this equation is
a Keplerian ellipse whose properties are fully determined after six integrals of the motion, known
as orbital elements, are specified.
Suppose that the aforementioned Keplerian orbit is slightly perturbed; for example, by the presence of a second planet orbiting the Sun. In this case, the planet's modified equation of motion takes the general form
where is a so-called disturbing function that fully describes the perturbation.
Adopting the standard Cartesian coordinate system
is a so-called disturbing function that fully describes the perturbation.
Adopting the standard Cartesian coordinate system 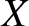 ,
, 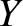 ,
,  , described in Section 4.12, we see that the preceding equation yields
where
, described in Section 4.12, we see that the preceding equation yields
where
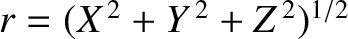 .
.
If the right-hand sides of Equations (G.3)–(G.5) are set to zero (i.e., if there is no perturbation) then we obtain a Keplerian orbit of the general form
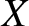 |
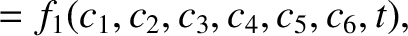 |
(G.6) |
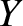 |
 |
(G.7) |
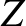 |
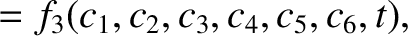 |
(G.8) |
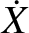 |
 |
(G.9) |
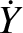 |
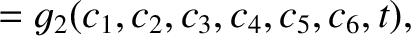 |
(G.10) |
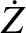 |
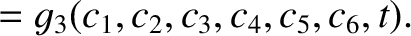 |
(G.11) |
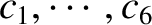 are the six constant elements that determine the orbit. (See Section 4.12.)
It follows that
for
are the six constant elements that determine the orbit. (See Section 4.12.)
It follows that
for 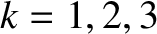 .
.
Let us now take the right-hand sides of Equations (G.3)–(G.5)
into account. In this case, the orbital elements,
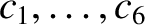 , are no longer
constants of the motion. However, provided the perturbation is sufficiently small, we would expect the elements to be relatively
slowly varying functions of time.
The purpose of this appendix is to derive evolution equations for these so-called osculating orbital elements.
Our approach is largely based on that of Brouwer and Clemence (1961).
, are no longer
constants of the motion. However, provided the perturbation is sufficiently small, we would expect the elements to be relatively
slowly varying functions of time.
The purpose of this appendix is to derive evolution equations for these so-called osculating orbital elements.
Our approach is largely based on that of Brouwer and Clemence (1961).