Next: Conservative fields Up: Useful mathematics Previous: Trigonometric identities
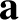 ,
, 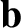 ,
, 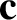 ,
, 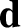 are general vectors;
are general vectors; 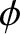 ,
, 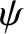 are general scalar fields;
are general scalar fields;
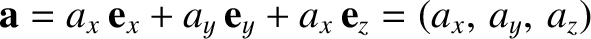 , and so on, where
, and so on, where 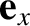 ,
, 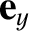 ,
and
,
and 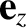 are right-handed Cartesian basis vectors.
are right-handed Cartesian basis vectors.
 |
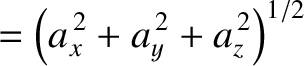 |
(A.73) |
 |
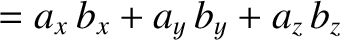 |
(A.74) |
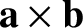 |
![$\displaystyle =\left\vert\begin{array}{ccc}{\bf e}_x,& {\bf e}_y,& {\bf e}_z\\ [0.5ex]
a_x,& a_y, &a_z\\ [0.5ex]
b_x,& b_y,& b_z
\end{array}\right\vert$](img3928.png) |
|
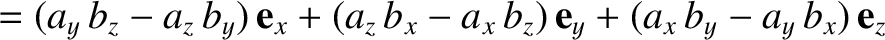 |
(A.75) | |
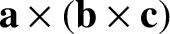 |
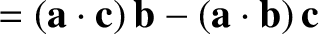 |
(A.76) |
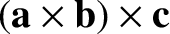 |
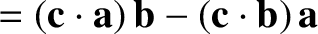 |
(A.77) |
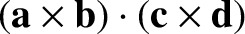 |
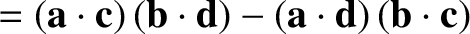 |
(A.78) |
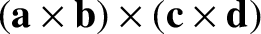 |
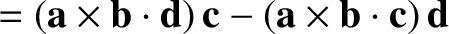 |
(A.79) |
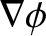 |
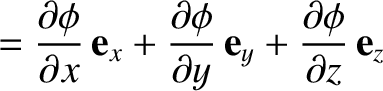 |
(A.80) |
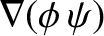 |
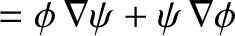 |
(A.81) |