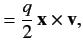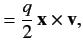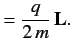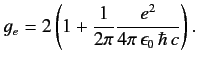

Next: Spin Precession
Up: Spin Angular Momentum
Previous: Rotation Operators in Spin
Magnetic Moments
Consider a particle of electric charge 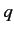 and speed
and speed 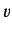 performing a circular orbit of radius
performing a circular orbit of radius 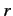 in the
in the 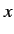 -
-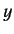 plane. The charge is equivalent to a current loop of radius
plane. The charge is equivalent to a current loop of radius 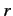 in the
in the 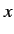 -
-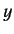 plane carrying current
plane carrying current
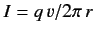 . The magnetic moment
. The magnetic moment
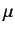 of
the loop is of magnitude
of
the loop is of magnitude
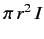 and is directed along the
and is directed along the 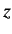 -axis.
Thus, we can write
-axis.
Thus, we can write
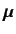 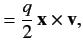 |
(458) |
where 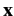 and
and 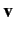 are the vector position and velocity of the particle,
respectively. However, we know that
are the vector position and velocity of the particle,
respectively. However, we know that
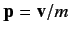 , where
, where 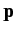 is the vector momentum of the particle, and
is the vector momentum of the particle, and 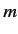 is its mass. We also know that
is its mass. We also know that
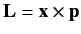 , where
, where 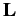 is the orbital angular momentum.
It follows that
is the orbital angular momentum.
It follows that
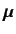 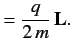 |
(459) |
Using the usual analogy between classical and quantum mechanics, we
expect the above relation to also hold between the quantum mechanical operators,
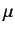 and
and 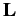 , which represent magnetic moment and orbital angular momentum,
respectively.
This is indeed found to the the case.
, which represent magnetic moment and orbital angular momentum,
respectively.
This is indeed found to the the case.
Spin angular momentum also gives rise to a contribution to the magnetic
moment of a charged particle. In fact, relativistic quantum
mechanics predicts that a charged particle possessing spin must also
possess a corresponding magnetic moment (this was first demonstrated by Dirac--see Chapter 11). We can write
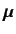 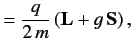 |
(460) |
where 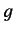 is called the gyromagnetic ratio. For an electron this ratio
is found to be
is called the gyromagnetic ratio. For an electron this ratio
is found to be
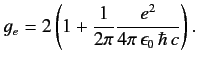 |
(461) |
The factor 2 is correctly predicted by Dirac's relativistic theory of the electron (see Chapter 11).
The small correction
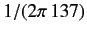 , derived originally by Schwinger, is due to
quantum field effects. We shall ignore this correction in the following,
so
, derived originally by Schwinger, is due to
quantum field effects. We shall ignore this correction in the following,
so
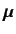 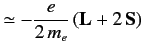 |
(462) |
for an electron (here, 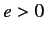 ).
).


Next: Spin Precession
Up: Spin Angular Momentum
Previous: Rotation Operators in Spin
Richard Fitzpatrick
2013-04-08