


Next: Eigenvalues and Eigenvectors
Up: Fundamental Concepts
Previous: Operators
So far, we have formed the following products:
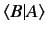 ,
,
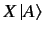 ,
,
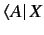 ,
, 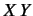 ,
,
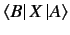 . Are there any other products
we are allowed to form? How about
. Are there any other products
we are allowed to form? How about
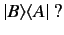 |
(39) |
This clearly depends linearly on the bra
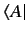 and the ket
and the ket  .
Suppose that we right-multiply the above product by the general ket
.
Suppose that we right-multiply the above product by the general ket
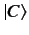 .
We obtain
.
We obtain
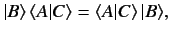 |
(40) |
since
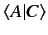 is just a number. Thus,
is just a number. Thus,
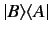 acting
on a general ket
acting
on a general ket 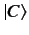 yields another ket. Clearly, the product
yields another ket. Clearly, the product
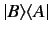 is a linear operator. This operator also acts on bras,
as is easily demonstrated by left-multiplying the expression (39) by a general
bra
is a linear operator. This operator also acts on bras,
as is easily demonstrated by left-multiplying the expression (39) by a general
bra
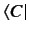 . It is also easily demonstrated that
. It is also easily demonstrated that
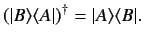 |
(41) |
Mathematicians term the operator
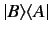 the outer product
of
the outer product
of
 and
and
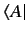 . The outer product should not be confused with
the inner product,
. The outer product should not be confused with
the inner product,
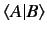 , which is just a number.
, which is just a number.



Next: Eigenvalues and Eigenvectors
Up: Fundamental Concepts
Previous: Operators
Richard Fitzpatrick
2013-04-08