

Next: Energy Levels of Hydrogen
Up: Orbital Angular Momentum
Previous: Eigenfunctions of Orbital Angular
Motion in Central Field
Consider a particle of mass  moving in a spherically symmetric potential.
The Hamiltonian takes the form
moving in a spherically symmetric potential.
The Hamiltonian takes the form
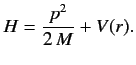 |
(387) |
Adopting Schrödinger's representation, we can write
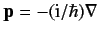 . Hence,
. Hence,
 |
(388) |
When written in spherical polar coordinates, the above equation becomes
![$\displaystyle H= -\frac{\hbar^2}{2\,M}\left[ \frac{1}{r^2}\frac{\partial}{\part...
...+ \frac{1}{r^2\sin^2\theta} \frac{\partial^2}{\partial\varphi^2}\right] + V(r).$](img927.png) |
(389) |
Comparing this equation with Equation (374), we find that
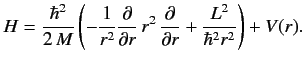 |
(390) |
Now, we know that the three components of angular momentum commute with  (see Section 4.1). We also know, from Equations (369)-(371), that
(see Section 4.1). We also know, from Equations (369)-(371), that 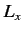 ,
, 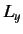 , and
, and 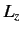 take the
form of partial derivative operators involving only angular coordinates,
when written in terms of spherical polar coordinates using the Schrödinger representation. It follows from Equation (390) that all three components of the angular
momentum commute with the Hamiltonian:
take the
form of partial derivative operators involving only angular coordinates,
when written in terms of spherical polar coordinates using the Schrödinger representation. It follows from Equation (390) that all three components of the angular
momentum commute with the Hamiltonian:
![$\displaystyle [{\bf L}, H] = 0.$](img929.png) |
(391) |
It is also easily seen that  (which can be expressed as a purely angular differential operator) commutes with the Hamiltonian:
(which can be expressed as a purely angular differential operator) commutes with the Hamiltonian:
![$\displaystyle [L^2, H] = 0.$](img930.png) |
(392) |
According to Section 3.2, the previous two equations
ensure that the angular momentum 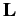 and its magnitude squared
and its magnitude squared  are both constants of the motion. This is as expected for a spherically
symmetric potential.
are both constants of the motion. This is as expected for a spherically
symmetric potential.
Consider the energy eigenvalue problem
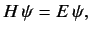 |
(393) |
where  is a number. Since
is a number. Since  and
and 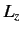 commute with each other and
the Hamiltonian, it is always possible to represent the state of the
system in terms of the simultaneous eigenstates of
commute with each other and
the Hamiltonian, it is always possible to represent the state of the
system in terms of the simultaneous eigenstates of  ,
, 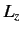 , and
, and 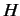 .
But, we already know that the most general form for the wavefunction of
a simultaneous
eigenstate of
.
But, we already know that the most general form for the wavefunction of
a simultaneous
eigenstate of  and
and 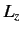 is (see previous section)
is (see previous section)
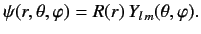 |
(394) |
Substituting Equation (394) into Equation (390), and making use of Equation (382), we
obtain
![$\displaystyle \left[\frac{\hbar^2}{2\,M} \left(-\frac{1}{r^2} \frac{d}{dr}\,r^2\,\frac{d}{dr} +\frac{l\,(l+1)}{r^2}\right) + V(r) - E\right] R = 0.$](img934.png) |
(395) |
This is a Sturm-Liouville equation for the function 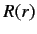 . We know,
from the general properties of this type of equation,
that if
. We know,
from the general properties of this type of equation,
that if 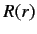 is required to be well-behaved at
is required to be well-behaved at 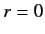 and as
and as
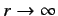 then solutions only exist for a discrete set of values of
then solutions only exist for a discrete set of values of  . These
are the energy eigenvalues. In general, the energy eigenvalues depend
on the quantum number
. These
are the energy eigenvalues. In general, the energy eigenvalues depend
on the quantum number  , but are independent of the quantum number
, but are independent of the quantum number 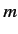 .
.


Next: Energy Levels of Hydrogen
Up: Orbital Angular Momentum
Previous: Eigenfunctions of Orbital Angular
Richard Fitzpatrick
2013-04-08
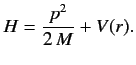
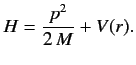

![$\displaystyle H= -\frac{\hbar^2}{2\,M}\left[ \frac{1}{r^2}\frac{\partial}{\part...
...+ \frac{1}{r^2\sin^2\theta} \frac{\partial^2}{\partial\varphi^2}\right] + V(r).$](img927.png)
![]() (see Section 4.1). We also know, from Equations (369)-(371), that
(see Section 4.1). We also know, from Equations (369)-(371), that ![]() ,
, ![]() , and
, and ![]() take the
form of partial derivative operators involving only angular coordinates,
when written in terms of spherical polar coordinates using the Schrödinger representation. It follows from Equation (390) that all three components of the angular
momentum commute with the Hamiltonian:
take the
form of partial derivative operators involving only angular coordinates,
when written in terms of spherical polar coordinates using the Schrödinger representation. It follows from Equation (390) that all three components of the angular
momentum commute with the Hamiltonian: