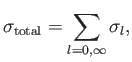Next: Determination of Phase-Shifts
Up: Scattering Theory
Previous: Partial Waves
Optical Theorem
The differential scattering cross-section,
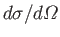 , is simply
the modulus squared of the scattering amplitude,
, is simply
the modulus squared of the scattering amplitude, 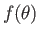 . [See Equation (10.28).] The
total scattering cross-section is defined as
. [See Equation (10.28).] The
total scattering cross-section is defined as
where
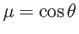 . It follows that
. It follows that
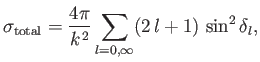 |
(10.89) |
where use has been made of Equation (10.65). A comparison of the preceding expression with
Equation (10.81) reveals that
![$\displaystyle \sigma_{\rm total} = \frac{4\pi}{k}\, {\rm Im}\left[f(0)\right] =\frac{4\pi}{k}\,{\rm Im}\left[f({\bf k},{\bf k})\right],$](img3578.png) |
(10.90) |
because
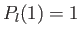 [1]. This result is known as the optical theorem [107,73],
and is a consequence of the fact that the very existence of scattering
requires scattering in the forward (
[1]. This result is known as the optical theorem [107,73],
and is a consequence of the fact that the very existence of scattering
requires scattering in the forward ( ) direction,
in order to interfere with the incident wave, and thereby reduce the
probability current in that direction.
) direction,
in order to interfere with the incident wave, and thereby reduce the
probability current in that direction.
It is conventional to write
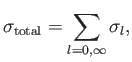 |
(10.91) |
where
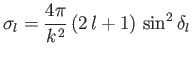 |
(10.92) |
is termed the 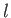 th partial scattering cross-section: that is, the contribution to the
total scattering cross-section from the
th partial scattering cross-section: that is, the contribution to the
total scattering cross-section from the 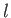 th partial wave. Note that (at fixed
th partial wave. Note that (at fixed 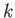 ) the maximum
value for the
) the maximum
value for the 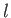 th partial scattering cross-section occurs when the associated phase-shift,
th partial scattering cross-section occurs when the associated phase-shift, 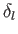 , takes the value
, takes the value 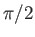 .
.



Next: Determination of Phase-Shifts
Up: Scattering Theory
Previous: Partial Waves
Richard Fitzpatrick
2016-01-22
![\begin{multline}
\sigma_{\rm total} = \oint d{\mit\Omega}\,\frac{d\sigma}{d{\mit...
... [0.5ex] \sin\delta_l \,\sin\delta_{l'}\,
P_l(\mu)\, P_{l'}(\mu),
\end{multline}](img3575.png)
![\begin{multline}
\sigma_{\rm total} = \oint d{\mit\Omega}\,\frac{d\sigma}{d{\mit...
... [0.5ex] \sin\delta_l \,\sin\delta_{l'}\,
P_l(\mu)\, P_{l'}(\mu),
\end{multline}](img3575.png)
![$\displaystyle \sigma_{\rm total} = \frac{4\pi}{k}\, {\rm Im}\left[f(0)\right] =\frac{4\pi}{k}\,{\rm Im}\left[f({\bf k},{\bf k})\right],$](img3578.png)