Let us take a surface  , that is not necessarily co-planar, and divide it up
into (scalar) elements
, that is not necessarily co-planar, and divide it up
into (scalar) elements
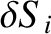 . Then
. Then
 |
(1.84) |
is a surface integral. For instance, the volume of water in a lake of depth
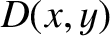 is
is
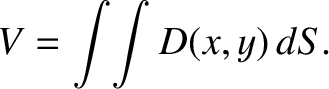 |
(1.85) |
To evaluate this integral, we must split the calculation into two ordinary integrals.
The volume in the strip shown in Figure A.17 is
![$\displaystyle \left[\int_{x_1}^{x_2} D(x,y)\,dx\right]dy.$](img4735.png) |
(1.86) |
Note that the limits 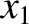 and
and 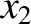 depend on
depend on  . The total volume is the sum
over all strips: that is,
. The total volume is the sum
over all strips: that is,
![$\displaystyle V = \int_{y_1}^{y_2} dy\left[\int_{x_1(y)}^{x_2(y)} D(x,y)\,dx\right]
\equiv \int\!\int_S D(x,y)\,dx\,dy.$](img4736.png) |
(1.87) |
Of course, the integral can be evaluated by taking the strips the other way around: that is,
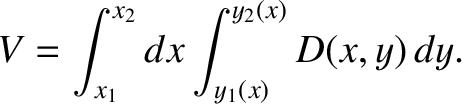 |
(1.88) |
Interchanging the order of integration is a very powerful and useful trick. But
great care must be taken when evaluating the limits.
Figure A.17:
Decomposition of a surface integral.
|
|
For example, consider
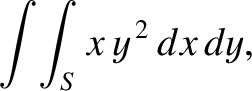 |
(1.89) |
where  is shown in Figure A.18.
Suppose that we evaluate the
is shown in Figure A.18.
Suppose that we evaluate the  integral first:
integral first:
![$\displaystyle dy\left(\int_0^{1-y} x\, y^{\,2}\,dx\right) = y^{\,2}\,dy\left[ \frac{x^{\,2}}{2}\right]^{1-y}_0
= \frac{y^{\,2}}{2}\,(1-y)^2\,dy.$](img4740.png) |
(1.90) |
Let us now evaluate the  integral:
integral:
 |
(1.91) |
We can also evaluate the integral by interchanging the order of integration:
 |
(1.92) |
In some cases, a surface integral is just the product of two separate integrals.
For instance,
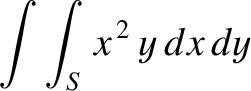 |
(1.93) |
where  is a unit square. This integral can be written
is a unit square. This integral can be written
 |
(1.94) |
because the limits are both independent of the other variable.
Figure A.18:
An example surface integral.
|
|
 , that is not necessarily co-planar, and divide it up
into (scalar) elements
, that is not necessarily co-planar, and divide it up
into (scalar) elements
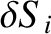 . Then
. Then

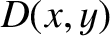 is
is
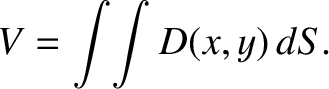
![$\displaystyle \left[\int_{x_1}^{x_2} D(x,y)\,dx\right]dy.$](img4735.png)
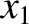 and
and 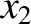 depend on
depend on  . The total volume is the sum
over all strips: that is,
. The total volume is the sum
over all strips: that is,
![$\displaystyle V = \int_{y_1}^{y_2} dy\left[\int_{x_1(y)}^{x_2(y)} D(x,y)\,dx\right]
\equiv \int\!\int_S D(x,y)\,dx\,dy.$](img4736.png)
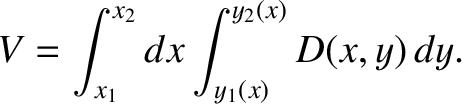
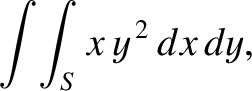
 is shown in Figure A.18.
Suppose that we evaluate the
is shown in Figure A.18.
Suppose that we evaluate the  integral first:
integral first:
![$\displaystyle dy\left(\int_0^{1-y} x\, y^{\,2}\,dx\right) = y^{\,2}\,dy\left[ \frac{x^{\,2}}{2}\right]^{1-y}_0
= \frac{y^{\,2}}{2}\,(1-y)^2\,dy.$](img4740.png)
 integral:
integral:


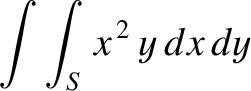
 is a unit square. This integral can be written
is a unit square. This integral can be written
