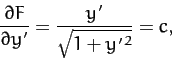Next: Conditional Variation
Up: Hamiltonian Dynamics
Previous: Introduction
Calculus of Variations
It is a well-known fact, first enunciated by Archimedes, that the shortest
distance between two points in a plane is a straight-line. However, suppose that
we wish to demonstrate this result from first principles. Let us consider the
length, 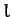 , of various curves,
, of various curves,  , which run between two fixed
points,
, which run between two fixed
points, 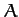 and
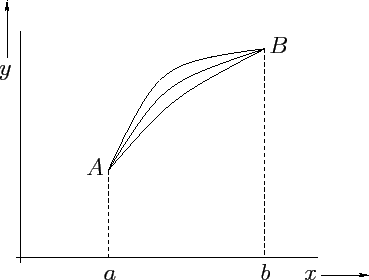
and 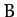 , in a plane, as illustrated in Figure 35. Now,
, in a plane, as illustrated in Figure 35. Now, 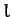 takes the form
takes the form
![\begin{displaymath}
l = \int_A^B [dx^2 + dy^2]^{1/2} = \int_a^b [1 + y'^{\,2}(x)]^{1/2}\,dx,
\end{displaymath}](img1717.png) |
(675) |
where
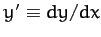 . Note that
. Note that 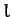 is a function of the function
is a function of the function  .
In mathematics, a function of a function is termed a functional.
.
In mathematics, a function of a function is termed a functional.
Figure 35:
Different paths between points 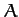 and
and  .
.
 |
Now, in order to find the shortest path between points  and
and  , we need to minimize the functional
, we need to minimize the functional 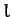 with respect to small variations
in the function
with respect to small variations
in the function  , subject to the constraint that the end points,
, subject to the constraint that the end points, 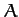 and
and 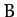 , remain fixed. In other words, we need to solve
, remain fixed. In other words, we need to solve
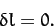 |
(676) |
The meaning of the above equation is that if
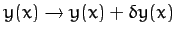 , where
, where 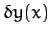 is small, then the first-order variation in
is small, then the first-order variation in 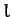 ,
denoted
,
denoted 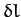 ,
vanishes. In other words,
,
vanishes. In other words,
 . The particular function
. The particular function
 for which
for which 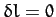 obviously yields an extremum of
obviously yields an extremum of 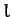 (i.e., either a maximum or a minimum). Hopefully,
in the case under consideration,
it yields a minimum of
(i.e., either a maximum or a minimum). Hopefully,
in the case under consideration,
it yields a minimum of 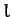 .
.
Consider a general functional of the form
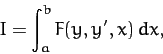 |
(677) |
where the end points of the integration are fixed.
Suppose that
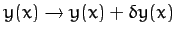 . The first-order variation in
. The first-order variation in 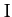 is written
is written
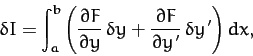 |
(678) |
where
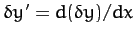 . Setting
. Setting  to zero, we
obtain
to zero, we
obtain
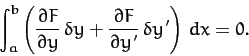 |
(679) |
This equation must be satisfied for all possible small perturbations 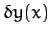 .
.
Integrating the second term in the integrand of the above equation by
parts, we get
![\begin{displaymath}
\int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\...
... +\left[\frac{\partial F}{\partial y'}\,\delta y\right]_a^b=0.
\end{displaymath}](img1731.png) |
(680) |
Now, if the end points are fixed then 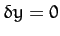 at
at
 and
and  . Hence, the last term on the left-hand side of the
above equation is zero. Thus, we obtain
. Hence, the last term on the left-hand side of the
above equation is zero. Thus, we obtain
![\begin{displaymath}
\int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)\right]\delta y\,dx =0.
\end{displaymath}](img1734.png) |
(681) |
The above equation must be satisfied for all small perturbations
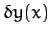 . The only way in which this is possible is for the
expression enclosed in square brackets in the integral to be zero. Hence, the functional
. The only way in which this is possible is for the
expression enclosed in square brackets in the integral to be zero. Hence, the functional
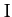 attains an extremum value whenever
attains an extremum value whenever
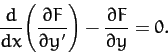 |
(682) |
This condition is known as the Euler-Lagrange equation.
Let us consider some special cases. Suppose that 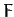 does not explicitly
depend on
does not explicitly
depend on  . It follows that
. It follows that
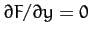 . Hence,
the Euler-Lagrange equation (682) simplifies to
. Hence,
the Euler-Lagrange equation (682) simplifies to
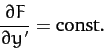 |
(683) |
Next, suppose that 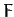 does not depend explicitly on
does not depend explicitly on  . Multiplying
Equation (682) by
. Multiplying
Equation (682) by 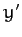 , we obtain
, we obtain
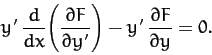 |
(684) |
However,
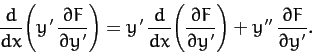 |
(685) |
Thus, we get
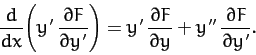 |
(686) |
Now, if 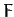 is not an explicit function of
is not an explicit function of  then the right-hand side of
the above equation is the total derivative of
then the right-hand side of
the above equation is the total derivative of 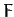 , namely
, namely 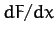 .
Hence, we obtain
.
Hence, we obtain
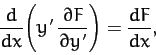 |
(687) |
which yields
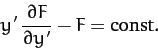 |
(688) |
Returning to the case under consideration, we have
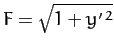 , according to Equation (675) and (677). Hence,
, according to Equation (675) and (677). Hence, 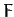 is not
an explicit function of
is not
an explicit function of  , so Equation (683) yields
, so Equation (683) yields
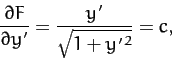 |
(689) |
where 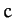 is a constant. So,
is a constant. So,
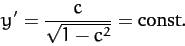 |
(690) |
Of course,
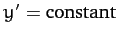 is the equation of a straight-line. Thus, the shortest distance between two fixed points in a plane is indeed a
straight-line.
is the equation of a straight-line. Thus, the shortest distance between two fixed points in a plane is indeed a
straight-line.



Next: Conditional Variation
Up: Hamiltonian Dynamics
Previous: Introduction
Richard Fitzpatrick
2011-03-31
![\begin{displaymath}
l = \int_A^B [dx^2 + dy^2]^{1/2} = \int_a^b [1 + y'^{\,2}(x)]^{1/2}\,dx,
\end{displaymath}](img1717.png)
![]() and
and ![]() , we need to minimize the functional
, we need to minimize the functional ![]() with respect to small variations
in the function
with respect to small variations
in the function ![]() , subject to the constraint that the end points,
, subject to the constraint that the end points, ![]() and
and ![]() , remain fixed. In other words, we need to solve
, remain fixed. In other words, we need to solve
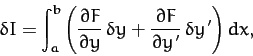
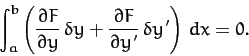
![\begin{displaymath}
\int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\...
... +\left[\frac{\partial F}{\partial y'}\,\delta y\right]_a^b=0.
\end{displaymath}](img1731.png)
![\begin{displaymath}
\int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)\right]\delta y\,dx =0.
\end{displaymath}](img1734.png)
![]() does not explicitly
depend on
does not explicitly
depend on ![]() . It follows that
. It follows that
![]() . Hence,
the Euler-Lagrange equation (682) simplifies to
. Hence,
the Euler-Lagrange equation (682) simplifies to
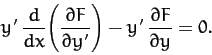
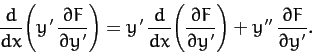
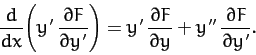
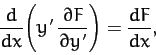
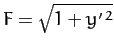 , according to Equation (675) and (677). Hence,
, according to Equation (675) and (677). Hence, ![]() is not
an explicit function of
is not
an explicit function of ![]() , so Equation (683) yields
, so Equation (683) yields