


Next: Exercises
Up: Rigid Body Rotation
Previous: Gyroscopic Precession
Consider a rigid body for which all of the principal moments of inertia
are distinct. Let
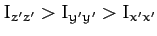 . Suppose that the
body is rotating freely about one of its principal axes. What happens when the
body is slightly disturbed?
. Suppose that the
body is rotating freely about one of its principal axes. What happens when the
body is slightly disturbed?
Let the body be initially rotating about the 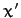 -axis, so that
-axis, so that
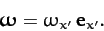 |
(577) |
If we apply a slight perturbation then the angular velocity becomes
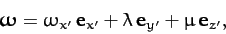 |
(578) |
where 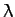 and
and 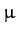 are both assumed to be small.
Euler's equations (504)-(506) take the
form
are both assumed to be small.
Euler's equations (504)-(506) take the
form
Since 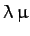 is second-order in small quantities--and, therefore, negligible--the first of the above equations tells us that
is second-order in small quantities--and, therefore, negligible--the first of the above equations tells us that 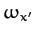 is an approximate constant of the motion. The other two equations
can be written
is an approximate constant of the motion. The other two equations
can be written
Differentiating the first equation with respect to time, and then eliminating
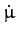 , we obtain
, we obtain
![\begin{displaymath}
\ddot{\lambda} + \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-...
...})}{I_{y'y'}\,I_{z'z'}}\right]\omega_{x'}^{\,2} \,\lambda = 0.
\end{displaymath}](img1543.png) |
(584) |
It is easily demonstrated that 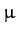 satisfies the same differential equation.
Since the term in square brackets in the above equation is positive,
the equation takes the form of a simple harmonic equation, and, thus,
has the bounded solution:
satisfies the same differential equation.
Since the term in square brackets in the above equation is positive,
the equation takes the form of a simple harmonic equation, and, thus,
has the bounded solution:
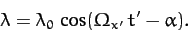 |
(585) |
Here, 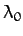 and
and 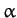 are constants of integration, and
are constants of integration, and
![\begin{displaymath}
{\mit\Omega}_{x'} = \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-I_{x'x'})}{I_{y'y'}\,I_{z'z'}}\right]^{1/2}\! \omega_{x'}.
\end{displaymath}](img1546.png) |
(586) |
Thus, the body oscillates sinusoidally about its initial state
with the angular frequency
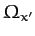 .
It follows that the body is stable to small perturbations
when rotating about the
.
It follows that the body is stable to small perturbations
when rotating about the 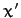 -axis, in the sense that the amplitude of
such perturbations does not grow in time.
-axis, in the sense that the amplitude of
such perturbations does not grow in time.
Suppose that the body is initially rotating about the 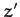 -axis, and
is subject to a small perturbation. A similar argument to the above allows
us to conclude that the body oscillates sinusoidally about its initial state
with angular frequency
-axis, and
is subject to a small perturbation. A similar argument to the above allows
us to conclude that the body oscillates sinusoidally about its initial state
with angular frequency
![\begin{displaymath}
{\mit\Omega}_{z'} = \left[\frac{(I_{z'z'}-I_{x'x'})\,(I_{z'z'}-I_{y'y'})}{I_{x'x'}\,I_{y'y'}}\right]^{1/2}\! \omega_{z'}.
\end{displaymath}](img1548.png) |
(587) |
Hence, the body is also stable to small perturbations when rotating about the
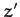 -axis.
-axis.
Suppose, finally, that the body is initially rotating about the 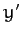 -axis,
and is subject to a small perturbation, such that
-axis,
and is subject to a small perturbation, such that
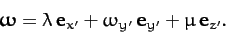 |
(588) |
It is easily demonstrated that 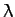 satisfies the following differential
equation:
satisfies the following differential
equation:
![\begin{displaymath}
\ddot{\lambda} - \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-...
...})}{I_{x'x'}\,I_{z'z'}}\right]\omega_{y'}^{\,2} \,\lambda = 0.
\end{displaymath}](img1550.png) |
(589) |
Note that the term in square brackets is positive. Hence, the
above equation is not the simple harmonic equation. Indeed
its solution takes the form
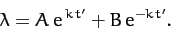 |
(590) |
Here, 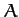 and
and 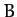 are constants of integration, and
are constants of integration, and
![\begin{displaymath}
k= \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-I_{y'y'})}{I_{x'x'}\,I_{z'z'}}\right]^{1/2}\omega_{y'}.
\end{displaymath}](img1552.png) |
(591) |
In this case, the amplitude of the perturbation grows exponentially in time.
Hence, the body is unstable to small perturbations
when rotating about the 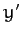 -axis.
-axis.
In conclusion, a rigid body with three distinct principal moments of inertia is stable to small perturbations when rotating about the
principal axes with the largest and smallest moments, but
is unstable when rotating about the axis with the intermediate
moment.
Finally, if two of the principal moments are the same then it can be shown
that the body is only stable to small perturbations when rotating
about the principal axis whose moment is distinct from the other two.



Next: Exercises
Up: Rigid Body Rotation
Previous: Gyroscopic Precession
Richard Fitzpatrick
2011-03-31
![]() -axis, so that
-axis, so that
![$\displaystyle \left[\frac{(I_{z'z'}-I_{x'x'})\,\omega_{x'}}{I_{y'y'}}\right]\mu,$](img1539.png)
![$\displaystyle - \left[\frac{(I_{y'y'}-I_{x'x'})\,\omega_{x'}}{I_{z'z'}}\right]\lambda.$](img1541.png)
![\begin{displaymath}
\ddot{\lambda} + \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-...
...})}{I_{y'y'}\,I_{z'z'}}\right]\omega_{x'}^{\,2} \,\lambda = 0.
\end{displaymath}](img1543.png)
![\begin{displaymath}
{\mit\Omega}_{x'} = \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-I_{x'x'})}{I_{y'y'}\,I_{z'z'}}\right]^{1/2}\! \omega_{x'}.
\end{displaymath}](img1546.png)
![]() -axis, and
is subject to a small perturbation. A similar argument to the above allows
us to conclude that the body oscillates sinusoidally about its initial state
with angular frequency
-axis, and
is subject to a small perturbation. A similar argument to the above allows
us to conclude that the body oscillates sinusoidally about its initial state
with angular frequency
![\begin{displaymath}
{\mit\Omega}_{z'} = \left[\frac{(I_{z'z'}-I_{x'x'})\,(I_{z'z'}-I_{y'y'})}{I_{x'x'}\,I_{y'y'}}\right]^{1/2}\! \omega_{z'}.
\end{displaymath}](img1548.png)
![]() -axis,
and is subject to a small perturbation, such that
-axis,
and is subject to a small perturbation, such that
![\begin{displaymath}
\ddot{\lambda} - \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-...
...})}{I_{x'x'}\,I_{z'z'}}\right]\omega_{y'}^{\,2} \,\lambda = 0.
\end{displaymath}](img1550.png)
![\begin{displaymath}
k= \left[\frac{(I_{y'y'}-I_{x'x'})\,(I_{z'z'}-I_{y'y'})}{I_{x'x'}\,I_{z'z'}}\right]^{1/2}\omega_{y'}.
\end{displaymath}](img1552.png)