


Next: Kepler's First Law
Up: Planetary Motion
Previous: Conic Sections
Multiplying our planet's tangential equation of motion, (229),
by 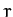 , we obtain
, we obtain
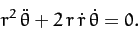 |
(245) |
However, the above equation can be also written
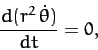 |
(246) |
which implies that
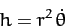 |
(247) |
is constant in time. It is easily demonstrated that 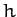 is the magnitude
of the vector
is the magnitude
of the vector 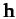 defined in Equation (216). Thus, the fact that
defined in Equation (216). Thus, the fact that
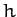 is constant in time is equivalent to the statement that the angular
momentum of our planet is a constant of its motion. As we have already mentioned, this is the case
because gravity is a central force.
is constant in time is equivalent to the statement that the angular
momentum of our planet is a constant of its motion. As we have already mentioned, this is the case
because gravity is a central force.
Figure 18:
Kepler's second law.
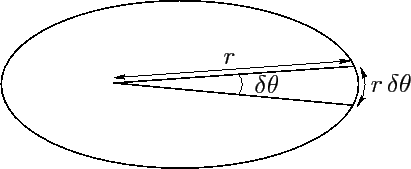 |
Suppose that the radius vector connecting our planet to the origin (i.e., the Sun) sweeps
out an angle 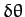 between times
between times 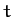 and
and 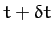 --see Figure 18. The approximately triangular region swept out by the radius vector has the area
--see Figure 18. The approximately triangular region swept out by the radius vector has the area
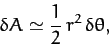 |
(248) |
since the area of a triangle is half its base (
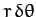 ) times its
height (
) times its
height (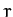 ). Hence, the rate at which the radius vector sweeps out area
is
). Hence, the rate at which the radius vector sweeps out area
is
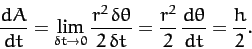 |
(249) |
Thus, the radius vector sweeps out area at a constant rate (since 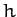 is
constant in time)--this is Kepler's second law. We conclude that Kepler's
second law of planetary motion is a direct consequence of angular
momentum conservation.
is
constant in time)--this is Kepler's second law. We conclude that Kepler's
second law of planetary motion is a direct consequence of angular
momentum conservation.



Next: Kepler's First Law
Up: Planetary Motion
Previous: Conic Sections
Richard Fitzpatrick
2011-03-31
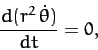
![]() between times
between times ![]() and
and ![]() --see Figure 18. The approximately triangular region swept out by the radius vector has the area
--see Figure 18. The approximately triangular region swept out by the radius vector has the area