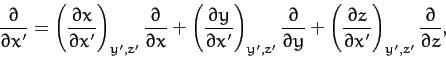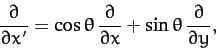

Next: Curvilinear Coordinates
Up: Vector Algebra and Vector
Previous: Gradient
Grad Operator
It is useful to define the vector operator
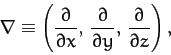 |
(1362) |
which is usually called the grad or del operator.
This operator acts on everything to
its right in a expression, until the end of the expression
or a closing bracket is reached.
For instance,
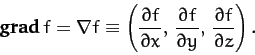 |
(1363) |
For two scalar fields 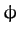 and
and 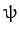 ,
,
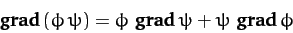 |
(1364) |
can be written more succinctly as
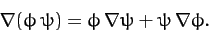 |
(1365) |
Suppose that we rotate the coordinate axes through an angle 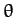 about
about 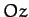 .
By analogy with Equations (A.1277)-(A.1279), the old coordinates (
.
By analogy with Equations (A.1277)-(A.1279), the old coordinates (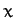 ,
, 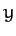 ,
, 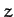 ) are related
to the new ones (
) are related
to the new ones (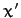 ,
, 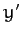 ,
, 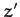 ) via
) via
Now,
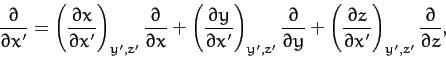 |
(1369) |
giving
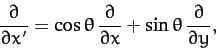 |
(1370) |
and
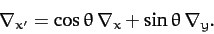 |
(1371) |
It can be seen, from Equations (A.1280)-(A.1282), that
the differential operator  transforms in an analogous manner to
a vector.
This is another proof that
transforms in an analogous manner to
a vector.
This is another proof that 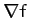 is a good vector.
is a good vector.
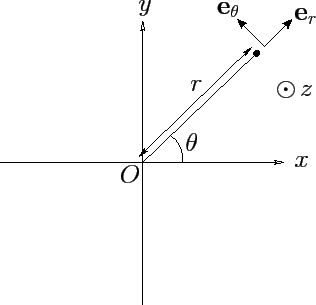
Figure A.113:
Cylindrical polar coordinates.
 |


Next: Curvilinear Coordinates
Up: Vector Algebra and Vector
Previous: Gradient
Richard Fitzpatrick
2011-03-31
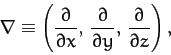
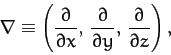
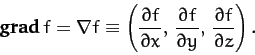
![]() about
about ![]() .
By analogy with Equations (A.1277)-(A.1279), the old coordinates (
.
By analogy with Equations (A.1277)-(A.1279), the old coordinates (![]() ,
, ![]() ,
, ![]() ) are related
to the new ones (
) are related
to the new ones (![]() ,
, ![]() ,
, ![]() ) via
) via