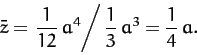Next: Gradient
Up: Vector Algebra and Vector
Previous: Vector Line Integrals
A volume integral takes the form
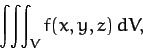 |
(1341) |
where 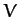 is some volume, and
is some volume, and
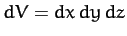 is a small volume element. The
volume element is sometimes written
is a small volume element. The
volume element is sometimes written 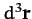 , or even
, or even  .
.
As an example
of a volume integral, let us evaluate the center of gravity of a solid pyramid. Suppose that
the pyramid has a square base of side 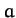 , a height
, a height 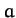 , and is composed of material of uniform density. Let the centroid of the base lie at the origin, and let
the apex lie at
, and is composed of material of uniform density. Let the centroid of the base lie at the origin, and let
the apex lie at 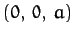 .
By symmetry, the center of mass lies on the line joining the centroid to the apex.
In fact, the height of the center of mass is given by
.
By symmetry, the center of mass lies on the line joining the centroid to the apex.
In fact, the height of the center of mass is given by
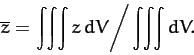 |
(1342) |
The bottom integral is just the volume of the pyramid, and can be written
Here, we have evaluated the  -integral last because the limits of the
-integral last because the limits of the  - and
- and  - integrals are
- integrals are  -dependent.
The top integral takes the form
-dependent.
The top integral takes the form
Thus,
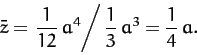 |
(1345) |
In other words, the center of mass of a pyramid lies one quarter of the way between the centroid of the base and the apex.



Next: Gradient
Up: Vector Algebra and Vector
Previous: Vector Line Integrals
Richard Fitzpatrick
2011-03-31
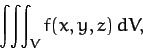
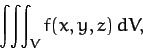
![]() , a height
, a height ![]() , and is composed of material of uniform density. Let the centroid of the base lie at the origin, and let
the apex lie at
, and is composed of material of uniform density. Let the centroid of the base lie at the origin, and let
the apex lie at ![]() .
By symmetry, the center of mass lies on the line joining the centroid to the apex.
In fact, the height of the center of mass is given by
.
By symmetry, the center of mass lies on the line joining the centroid to the apex.
In fact, the height of the center of mass is given by
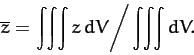
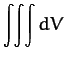
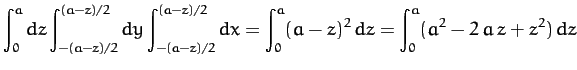
![$\displaystyle \left[a^2\,z-a\,z^2+z^3/3\right]_0^a= \frac{1}{3}\,a^3.$](img3426.png)
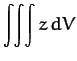
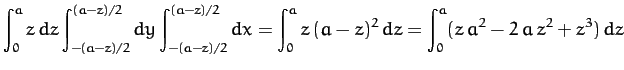
![$\displaystyle \left[a^2\,z^2/2-2\,a\,z^3/3+z^4/4\right]_0^a= \frac{1}{12}\,a^4.$](img3429.png)