


Next: Co-Rotating Frame
Up: The Three-Body Problem
Previous: Jacobi Integral
Consider a dynamical system consisting of three gravitationally
interacting point masses, 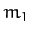 ,
, 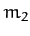 , and
, and 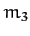 . Let mass
. Let mass 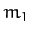 represent the Sun, mass
represent the Sun, mass 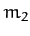 the planet Jupiter, and mass
the planet Jupiter, and mass 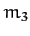 a comet. Since the
mass of a comet is very much less than that of the Sun or Jupiter, and the Sun and Jupiter
are in (almost) circular orbits about their common center of mass, the dynamical system in question satisfies
all of the necessary criteria to be considered an example of a restricted three-body problem.
a comet. Since the
mass of a comet is very much less than that of the Sun or Jupiter, and the Sun and Jupiter
are in (almost) circular orbits about their common center of mass, the dynamical system in question satisfies
all of the necessary criteria to be considered an example of a restricted three-body problem.
Now, the mass of the Sun is much greater than that of Jupiter. It follows that the gravitational
effect of Jupiter on the cometary orbit is negligible unless the comet makes a very close
approach to Jupiter. Hence, as described in Chapter 5, before and after such an approach, the comet executes a
standard elliptical orbit about the Sun with fixed orbital parameters: i.e., fixed major radius, eccentricity, and
inclination to the ecliptic plane. However, in general, the orbital parameters before and after the close approach will not be the same
as one another. Let us investigate further.
Now, since 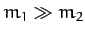 , we have
, we have
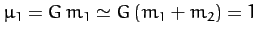 , and
, and
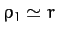 .
Hence, according to Equations (260) and (269), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
.
Hence, according to Equations (260) and (269), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
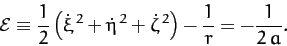 |
(1045) |
Note that the comet's orbital energy is entirely determined by its major radius, 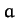 . (Incidentally, we are working
in units such that the major radius of Jupiter's orbit is unity.) Furthermore, the (approximately) conserved
angular momentum (per unit mass) of the comet before and after its approach to Jupiter
is written
. (Incidentally, we are working
in units such that the major radius of Jupiter's orbit is unity.) Furthermore, the (approximately) conserved
angular momentum (per unit mass) of the comet before and after its approach to Jupiter
is written 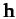 , where
, where 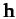 is directed normal to the comet's orbital plane,
and, from Equations (236) and (256),
is directed normal to the comet's orbital plane,
and, from Equations (236) and (256),
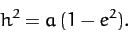 |
(1046) |
Here, 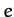 is the comet's orbital eccentricity. It follows that
is the comet's orbital eccentricity. It follows that
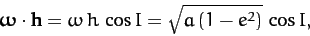 |
(1047) |
since 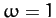 in our adopted system of units. Here,
in our adopted system of units. Here, 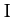 is the angle of
inclination of the normal to the comet's orbital plane to that of Jupiter's orbital
plane.
is the angle of
inclination of the normal to the comet's orbital plane to that of Jupiter's orbital
plane.
Let 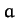 ,
, 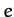 , and
, and 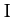 be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let
be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let 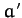 ,
, 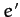 , and
, and 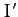 be the corresponding
parameters after the encounter. It follows from Equations (1044), (1045), and
(1047), and the fact that
be the corresponding
parameters after the encounter. It follows from Equations (1044), (1045), and
(1047), and the fact that 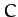 is conserved during the encounter, whereas
is conserved during the encounter, whereas
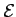 and
and 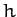 are not, that
are not, that
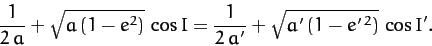 |
(1048) |
This result is known as the Tisserand criterion, and restricts the possible changes in the
orbital parameters of a comet due to a close encounter with Jupiter (or any other
massive planet).
The Tisserand criterion is very useful. For instance, whenever a new comet is discovered, astronomers
immediately calculate its Tisserand parameter,
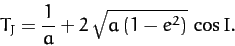 |
(1049) |
If this parameter has the same value as that of a previously observed comet then it
is quite likely that the new comet is, in fact, the same comet, but that
its orbital parameters have changed since it was last observed, due to a close encounter with Jupiter. Incidentally,
the subscript 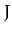 in the above formula is to remind us that we are dealing with the
Tisserand parameter for close encounters with Jupiter. (The parameter is, thus, evaluated
in a system of units in which the major radius of Jupiter's orbit is unity). Obviously,
it is also possible to calculate Tisserand parameters for close encounters with other planets.
in the above formula is to remind us that we are dealing with the
Tisserand parameter for close encounters with Jupiter. (The parameter is, thus, evaluated
in a system of units in which the major radius of Jupiter's orbit is unity). Obviously,
it is also possible to calculate Tisserand parameters for close encounters with other planets.
The Tisserand criterion is also applicable to so-called gravity assists, in which a
space-craft gains energy due to a close encounter with a moving planet. Such assists
are often employed in missions to the outer planets to reduce the amount of fuel
which the space-craft must carry in order to reach its destination. In fact, it is clear,
from Equations (1045) and (1048), that a space-craft can make use of a close encounter
with a moving planet to increase (or decrease) its orbital major radius 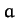 , and, hence, to increase
(or decrease)
its total orbital energy.
, and, hence, to increase
(or decrease)
its total orbital energy.



Next: Co-Rotating Frame
Up: The Three-Body Problem
Previous: Jacobi Integral
Richard Fitzpatrick
2011-03-31
![]() , we have
, we have
![]() , and
, and
![]() .
Hence, according to Equations (260) and (269), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
.
Hence, according to Equations (260) and (269), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
![]() ,
, ![]() , and
, and ![]() be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let
be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let ![]() ,
, ![]() , and
, and ![]() be the corresponding
parameters after the encounter. It follows from Equations (1044), (1045), and
(1047), and the fact that
be the corresponding
parameters after the encounter. It follows from Equations (1044), (1045), and
(1047), and the fact that ![]() is conserved during the encounter, whereas
is conserved during the encounter, whereas
![]() and
and ![]() are not, that
are not, that
![]() , and, hence, to increase
(or decrease)
its total orbital energy.
, and, hence, to increase
(or decrease)
its total orbital energy.