


Next: Rotational Kinetic Energy
Up: Rigid Body Rotation
Previous: Fundamental Equations
Moment of Inertia Tensor
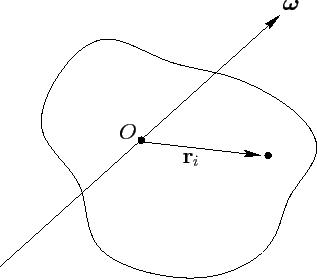
Consider a rigid body rotating with fixed angular velocity 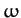 about
an axis which passes through the origin--see Figure 28.
Let
about
an axis which passes through the origin--see Figure 28.
Let 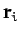 be the position vector of the
be the position vector of the 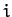 th mass element, whose mass
is
th mass element, whose mass
is 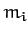 .
We expect this position vector to precess about the axis of rotation
(which is parallel to
.
We expect this position vector to precess about the axis of rotation
(which is parallel to 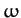 )
with angular velocity
)
with angular velocity 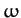 . It, therefore, follows from Equation (A.1309)
that
. It, therefore, follows from Equation (A.1309)
that
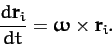 |
(457) |
Thus, the above equation specifies the velocity,
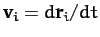 ,
of each mass element as the body rotates with fixed angular velocity
,
of each mass element as the body rotates with fixed angular velocity 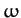 about
an axis passing through the origin.
about
an axis passing through the origin.
Figure 28:
A rigid rotating body.
 |
The total angular momentum of the body (about the origin) is written
![\begin{displaymath}
{\bf L} = \sum_{i=1,N} m_i\,{\bf r}_i\times\frac{d{\bf r}_i}...
...}- ({\bf r}_i\cdot\mbox{\boldmath$\omega$})\,{\bf r}_i\right],
\end{displaymath}](img1241.png) |
(458) |
where use has been made of Equation (457), and some standard vector
identities (see Section A.10). The above formula can be written as a matrix equation
of the form
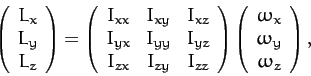 |
(459) |
where
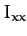 |
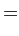 |
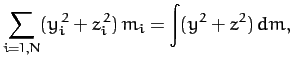 |
(460) |
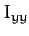 |
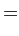 |
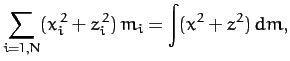 |
(461) |
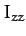 |
 |
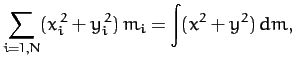 |
(462) |
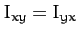 |
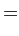 |
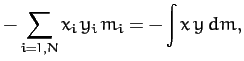 |
(463) |
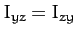 |
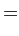 |
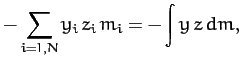 |
(464) |
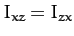 |
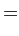 |
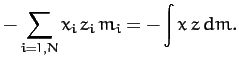 |
(465) |
Here, 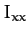 is called the moment of inertia about the
is called the moment of inertia about the  -axis,
-axis,
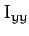 the moment of inertia about the
the moment of inertia about the 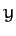 -axis,
-axis, 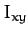 the
the 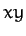 product of inertia,
product of inertia, 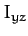 the
the 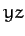 product of
inertia, etc. The matrix of the
product of
inertia, etc. The matrix of the 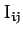 values is
known as the moment of inertia tensor.
values is
known as the moment of inertia tensor.![[*]](footnote.png) Note that each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals,
Note that each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals, 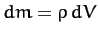 , where
, where 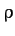 is the mass density, and
is the mass density, and
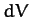 a volume element.
Equation (459) can be written more succinctly as
a volume element.
Equation (459) can be written more succinctly as
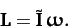 |
(466) |
Here, it is understood that 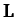 and
and 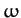 are
both column vectors, and
are
both column vectors, and 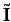 is the matrix of the
is the matrix of the 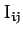 values.
Note that
values.
Note that 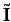 is a real symmetric matrix:
i.e.,
is a real symmetric matrix:
i.e.,
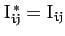 and
and
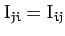 .
.
In general,
the angular momentum vector, 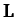 , obtained from Equation (466),
points in a different direction to the angular velocity vector,
, obtained from Equation (466),
points in a different direction to the angular velocity vector, 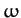 . In other words,
. In other words, 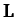 is generally not parallel to
is generally not parallel to 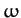 .
.
Finally, although the above results were obtained assuming a
fixed angular velocity, they remain valid at each instant in time if the angular velocity varies.



Next: Rotational Kinetic Energy
Up: Rigid Body Rotation
Previous: Fundamental Equations
Richard Fitzpatrick
2011-03-31
![[*]](footnote.png) Note that each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals,
Note that each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals, ![]() , obtained from Equation (466),
points in a different direction to the angular velocity vector,
, obtained from Equation (466),
points in a different direction to the angular velocity vector, ![]() . In other words,
. In other words, ![]() is generally not parallel to
is generally not parallel to ![]() .
.