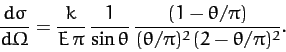Next: Rotating Reference Frames
Up: Two-Body Dynamics
Previous: Scattering in the Laboratory
- A particle subject to a repulsive force varying as
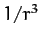 is projected from infinity with a velocity
that would carry it to a distance
is projected from infinity with a velocity
that would carry it to a distance 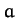 from the center of force, if it were directed toward the latter. Actually, it
is projected along a line whose closest distance from the center of force would be
from the center of force, if it were directed toward the latter. Actually, it
is projected along a line whose closest distance from the center of force would be 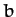 if there were no repulsion. Prove that the
particle's least distance from
the center is
if there were no repulsion. Prove that the
particle's least distance from
the center is
 , and that the angle between the two asymptotes of its path
is
, and that the angle between the two asymptotes of its path
is
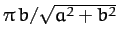 .
.
- A particle subject to a repulsive force varying as
 is projected from infinity with a velocity
is projected from infinity with a velocity 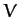 that
would carry it to a distance
that
would carry it to a distance 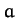 from the center of force, if it were directed toward the latter. Actually, it
is projected along a line whose closest distance from the center of force would be
from the center of force, if it were directed toward the latter. Actually, it
is projected along a line whose closest distance from the center of force would be 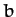 if there were no repulsion.
Show that the least velocity of the particle is
if there were no repulsion.
Show that the least velocity of the particle is
- Using the notation of Section 6.2, show that
the angular momentum of a two-body system takes the
form
where  .
.
- Consider the case of Rutherford scattering in the event that
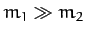 . Demonstrate that the differential scattering cross-section in the
laboratory frame is approximately
. Demonstrate that the differential scattering cross-section in the
laboratory frame is approximately
where
 .
.
- Show that the energy distribution of particles recoiling from an elastic
collision is always directly proportional to the differential scattering cross-section
in the center of mass frame.
- It is found experimentally that in the elastic scattering of neutrons
by protons (
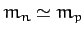 ) at relatively low energies the energy distribution
of the recoiling protons in the laboratory frame is constant up to
a maximum energy, which is the energy of the incident neutrons. What is the
angular distribution of the scattering in the center of mass frame?
) at relatively low energies the energy distribution
of the recoiling protons in the laboratory frame is constant up to
a maximum energy, which is the energy of the incident neutrons. What is the
angular distribution of the scattering in the center of mass frame?
- The most energetic
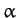 -particles available to Earnst Rutherford and his colleagues for the
famous Rutherford scattering experiment were
-particles available to Earnst Rutherford and his colleagues for the
famous Rutherford scattering experiment were  MeV. For the scattering of 7.7MeV
MeV. For the scattering of 7.7MeV 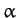 -particles from Uranium 238 nuclei (initially at rest) at a scattering angle in the laboratory frame of
-particles from Uranium 238 nuclei (initially at rest) at a scattering angle in the laboratory frame of
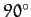 , find the following (in the laboratory frame, unless otherwise specified):
, find the following (in the laboratory frame, unless otherwise specified):
- The recoil scattering angle of the Uranium nucleus.
- The scattering angles of the
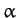 -particle and Uranium nucleus in the center of mass
frame.
-particle and Uranium nucleus in the center of mass
frame.
- The kinetic energies of the scattered
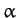 -particle and Uranium nucleus (in MeV).
-particle and Uranium nucleus (in MeV).
- The impact parameter,
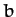 .
.
- The distance of closest approach.
- The differential scattering cross-section at
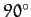 .
.
- Consider scattering by the repulsive potential
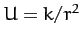 (where
(where 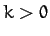 )
viewed in the center of mass frame. Demonstrate that the differential
scattering cross-section is
)
viewed in the center of mass frame. Demonstrate that the differential
scattering cross-section is



Next: Rotating Reference Frames
Up: Two-Body Dynamics
Previous: Scattering in the Laboratory
Richard Fitzpatrick
2011-03-31
![\begin{displaymath}
V\,\frac{b^2}{a^2}\left[\left(\frac{a^4}{b^4}+\frac{1}{4}\right)^{1/2}-\frac{1}{2}\right]^{1/2}.
\end{displaymath}](img1095.png)
![\begin{displaymath}
\frac{d\sigma}{d\Omega'}\simeq \frac{q_1^{\,2}\,q_2^{\,2}}{4...
...rm max})^2}]^2\,\left[1-(\psi/\psi_{\rm max})^2\right]^{1/2}},
\end{displaymath}](img1098.png)
 -particle and Uranium nucleus in the center of mass
frame.
-particle and Uranium nucleus in the center of mass
frame.
 -particle and Uranium nucleus (in MeV).
-particle and Uranium nucleus (in MeV).
 .
.
 .
.