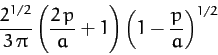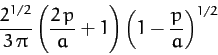Next: Two-Body Dynamics
Up: Planetary Motion
Previous: Motion in a Nearly
- Halley's comet has an orbital eccentricity of
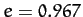 and a perihelion
distance of
and a perihelion
distance of 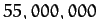 miles. Find the orbital period, and the comet's speed at
perihelion and aphelion.
miles. Find the orbital period, and the comet's speed at
perihelion and aphelion.
- A comet is first seen at a distance of
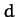 astronomical units (1 astronomical unit is the mean Earth-Sun distance) from the Sun, and
is traveling with a speed of
astronomical units (1 astronomical unit is the mean Earth-Sun distance) from the Sun, and
is traveling with a speed of 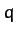 times the Earth's mean speed. Show that the orbit of the
comet is hyperbolic, parabolic, or elliptical, depending on whether the quantity
times the Earth's mean speed. Show that the orbit of the
comet is hyperbolic, parabolic, or elliptical, depending on whether the quantity 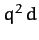 is
greater than, equal to, or less than 2, respectively.
is
greater than, equal to, or less than 2, respectively.
- Consider a planet in a Keplerian orbit of major radius
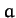 and
eccentricity
and
eccentricity 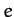 about the Sun. Suppose that the eccentricity of the orbit is small
(i.e.,
about the Sun. Suppose that the eccentricity of the orbit is small
(i.e., 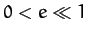 ), as is indeed the case for all of the planets except Mercury
and Pluto. Demonstrate that, to first-order in
), as is indeed the case for all of the planets except Mercury
and Pluto. Demonstrate that, to first-order in 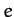 , the orbit can be approximated as a circle whose center is shifted a distance
, the orbit can be approximated as a circle whose center is shifted a distance 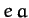 from
the Sun, and that the planet's angular motion appears uniform when
viewed from a point (called the Equant) which is shifted a distance
from
the Sun, and that the planet's angular motion appears uniform when
viewed from a point (called the Equant) which is shifted a distance
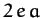 from the Sun, in the same direction as the center of the circle.
This theorem is the
basis of the Ptolomaic model of planetary motion.
from the Sun, in the same direction as the center of the circle.
This theorem is the
basis of the Ptolomaic model of planetary motion.
- How long (in days) does it take the Sun-Earth radius vector to
rotate through
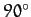 , starting at the perihelion point? How long does it take starting at the aphelion point? The period and eccentricity of the Earth's orbit are
, starting at the perihelion point? How long does it take starting at the aphelion point? The period and eccentricity of the Earth's orbit are 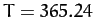 days, and
days, and 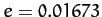 , respectively.
, respectively.
- Solve the Kepler problem for a parabolic orbit to obtain Equations (293)-(295).
- Solve the Kepler problem for a hyperbolic orbit to obtain Equations (296)-(298).
- A comet is in a parabolic orbit lying in the plane of the Earth's
orbit. Regarding the Earth's orbit as a circle of radius
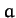 , show that the points
where the comet intersects the Earth's orbit are given by
, show that the points
where the comet intersects the Earth's orbit are given by
where 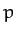 is the perihelion distance of the comet, defined at
is the perihelion distance of the comet, defined at 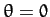 .
Show that the time interval that the comet remains inside the Earth's orbit is the
faction
.
Show that the time interval that the comet remains inside the Earth's orbit is the
faction
of a year, and that the maximum value of this time interval is 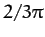 year, or
about 11 weeks.
year, or
about 11 weeks.
- Prove that in the case of a central force varying inversely as the cube of the
distance
where 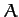 ,
, 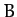 ,
, 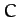 are constants.
are constants.
- The orbit of a particle moving in a central field is a circle passing
through the origin, namely
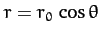 . Show that the force law
is inverse-fifth power.
. Show that the force law
is inverse-fifth power.
- A particle moving in a central field describes a spiral orbit
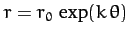 .
Show that the force law is inverse-cube, and that
.
Show that the force law is inverse-cube, and that 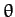 varies logarithmically with
varies logarithmically with 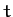 .
Show that there are two other possible types of orbit in this force-field, and give their
equations.
.
Show that there are two other possible types of orbit in this force-field, and give their
equations.
- A particle moves in a spiral orbit given by
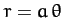 . Suppose that
. Suppose that 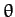 increases linearly
with
increases linearly
with 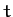 . Is the force acting on the particle central in nature? If not, determine how
. Is the force acting on the particle central in nature? If not, determine how 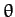 would have to
vary with
would have to
vary with 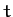 in order to make the force central.
in order to make the force central.
- A particle moves in a circular orbit of radius
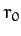 in an attractive
central force-field of the form
in an attractive
central force-field of the form
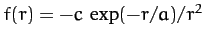 , where
, where 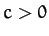 and
and 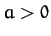 .
Demonstrate that the orbit is only stable provided that
.
Demonstrate that the orbit is only stable provided that 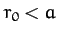 .
.
- A particle moves in a circular orbit in an attractive
central force-field of the form
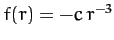 , where
, where 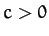 . Demonstrate
that the orbit is unstable to small perturbations.
. Demonstrate
that the orbit is unstable to small perturbations.
- If the Solar System were embedded in a uniform dust cloud, what would the apsidal angle
of a planet be for motion in a nearly circular orbit? Express your answer in terms of the ratio of the mass of dust contained in a sphere, centered on the Sun, whose radius is that of the orbit, to the mass of the Sun.
This model was once suggested as a possible
explanation for the advance of the perihelion of Mercury.
- The potential energy per unit mass of a particle in the gravitational
field of an oblate spheroid, like the Earth, is
where 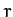 refers to distances in the equatorial plane,
refers to distances in the equatorial plane, 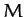 is the Earth's mass, and
is the Earth's mass, and
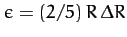 . Here,
. Here,
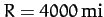 is the Earth's equatorial radius, and
is the Earth's equatorial radius, and
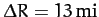 the difference between the equatorial and polar radii.
Find the apsidal angle for a satellite moving in a nearly circular orbit in the equatorial
plane of the Earth.
the difference between the equatorial and polar radii.
Find the apsidal angle for a satellite moving in a nearly circular orbit in the equatorial
plane of the Earth.



Next: Two-Body Dynamics
Up: Planetary Motion
Previous: Motion in a Nearly
Richard Fitzpatrick
2011-03-31