

Next: Line Integrals
Up: Vector Algebra and Vector
Previous: Vector Triple Product
Vector Calculus
Suppose that vector 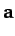 varies with time, so that
varies with time, so that
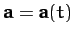 . The time
derivative of the vector is defined
. The time
derivative of the vector is defined
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img3364.png) |
(1320) |
When written out in component form this becomes
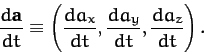 |
(1321) |
Suppose that 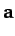 is, in fact, the product of a scalar
is, in fact, the product of a scalar 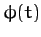 and another vector
and another vector
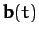 . What now is the time derivative of
. What now is the time derivative of 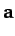 ? We have
? We have
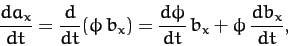 |
(1322) |
which implies that
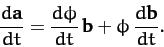 |
(1323) |
Moreover, it is easily demonstrated that
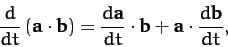 |
(1324) |
and
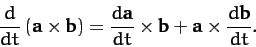 |
(1325) |
Hence, it can be seen that the laws of vector differentiation are analogous to those in
conventional calculus.


Next: Line Integrals
Up: Vector Algebra and Vector
Previous: Vector Triple Product
Richard Fitzpatrick
2011-03-31
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img3364.png)
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img3364.png)
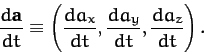
![]() is, in fact, the product of a scalar
is, in fact, the product of a scalar ![]() and another vector
and another vector
![]() . What now is the time derivative of
. What now is the time derivative of ![]() ? We have
? We have