


Next: Perihelion Precession of Mercury
Up: Gravitational Potential Theory
Previous: Potential Due to a
Perihelion Precession of the Planets
The Solar System consists of eight major planets (Mercury to Neptune) moving around the Sun in slightly elliptical orbits which are approximately
co-planar with one another. According to Chapter 5, if we neglect the relatively weak interplanetary
gravitational interactions then the perihelia of the various planets (i.e., the points on their orbits at which they are closest to the Sun) remain fixed in space. However, once these
interactions are taken into account, it turns out that the planetary perihelia all
slowly precess around the Sun. We can calculate the approximate rate of perihelion precession
of a given planet by treating the other planets as uniform concentric rings, centered on the Sun, of mass equal to the planetary mass, and
radius equal to the mean orbital radius.![[*]](footnote.png) This is equivalent to averaging the interplanetary gravitational interactions
over the orbits of the other planets. It is reasonable to do this, since the precession period in question is
very much longer than the orbital period of any planet in the Solar System. Thus, by treating the other planets as
rings, we can calculate the mean gravitational perturbation due to these planets, and, thereby, determine the
desired precession rate.
This is equivalent to averaging the interplanetary gravitational interactions
over the orbits of the other planets. It is reasonable to do this, since the precession period in question is
very much longer than the orbital period of any planet in the Solar System. Thus, by treating the other planets as
rings, we can calculate the mean gravitational perturbation due to these planets, and, thereby, determine the
desired precession rate.
We can conveniently index the planets in the Solar System such that Mercury is planet 1, and Neptune planet 8. Let the 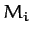 and the
and the 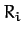 , for
, for 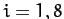 , be the planetary masses and orbital radii, respectively. Furthermore, let
, be the planetary masses and orbital radii, respectively. Furthermore, let 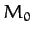 be the mass of the Sun.
It follows, from the previous section, that the gravitational potential generated at the
be the mass of the Sun.
It follows, from the previous section, that the gravitational potential generated at the 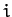 th planet by the Sun and
the other planets is
th planet by the Sun and
the other planets is
Now, the radial force per unit mass acting on the 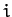 th planet is written
th planet is written
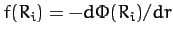 , giving
, giving
Hence, we obtain
where 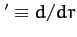 . It follows that
. It follows that
| |
|
![$\displaystyle \left[3 + \frac{R_i\,f'(R_i)}{f(R_i)}\right]^{-1/2} =1 + \frac{3}...
..._j}{R_i}\right)^2 + \frac{175}{64}\left(\frac{R_j}{R_i}
\right)^4+\cdots\right]$](img2405.png) |
|
| |
|
![$\displaystyle + \frac{3}{4}\sum_{j>i}\left(\frac{M_j}{M_0}\right)
\left(\frac{R...
...i}{R_j}\right)^2 + \frac{175}{64}\left(\frac{R_i}{R_j}
\right)^4+\cdots\right].$](img2406.png) |
(1021) |
Thus, according to Equation (317), the apsidal angle for the 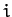 th planet is
th planet is
Hence, the perihelion of the 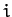 th planet advances by
th planet advances by
radians per revolution around the Sun. Now, the time for one revolution is
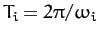 , where
, where
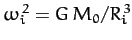 . Thus, the rate of perihelion precession, in arc seconds per year, is given by
. Thus, the rate of perihelion precession, in arc seconds per year, is given by
Table 1:
Data for the major planets in the Solar System, giving the planetary mass relative to that of the Sun, the orbital period in years, and the mean orbital
radius relative to that of the Earth.
| Planet |
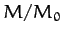 |
 |
R( au) |
| |
|
|
|
| Mercury |
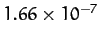 |
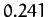 |
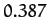 |
| Venus |
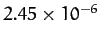 |
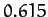 |
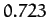 |
| Earth |
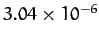 |
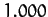 |
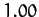 |
| Mars |
 |
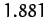 |
 |
| Jupiter |
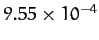 |
 |
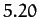 |
| Saturn |
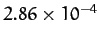 |
 |
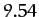 |
| Uranus |
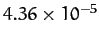 |
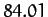 |
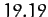 |
| Neptune |
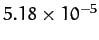 |
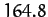 |
 |
|
Table 2:
The observed perihelion precession rates of the planets compared with the theoretical precession rates calculated from Equation (1024)
and Table 1. The precession rates are in arc seconds per year.
| |
|
|
| Planet |
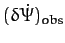 |
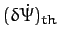 |
| Mercury |
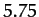 |
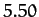 |
| Venus |
 |
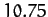 |
| Earth |
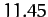 |
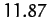 |
| Mars |
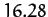 |
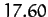 |
| Jupiter |
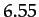 |
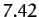 |
| Saturn |
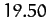 |
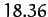 |
| Uranus |
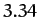 |
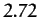 |
| Neptune |
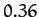 |
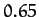 |
|
Figure 46:
The triangular points show the observed perihelion precession rates of the
major planets in the Solar System, whereas the square points show the theoretical
rates calculated from Equation (1024)
and Table 1. The precession rates are in arc seconds per
year.
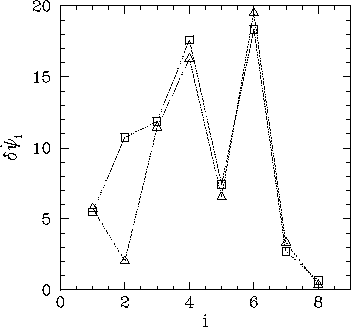 |
Table 2 and Figure 46 compare the observed perihelion precession rates
with the theoretical rates calculated from Equation (1024)
and the planetary data given in Table 1. It can be seen that there is excellent agreement
between the two, except for the planet Venus. The main reason for this is that Venus
has an unusually low eccentricity (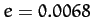 ), which renders its perihelion point extremely sensitive to small perturbations.
), which renders its perihelion point extremely sensitive to small perturbations.



Next: Perihelion Precession of Mercury
Up: Gravitational Potential Theory
Previous: Potential Due to a
Richard Fitzpatrick
2011-03-31
![[*]](footnote.png) This is equivalent to averaging the interplanetary gravitational interactions
over the orbits of the other planets. It is reasonable to do this, since the precession period in question is
very much longer than the orbital period of any planet in the Solar System. Thus, by treating the other planets as
rings, we can calculate the mean gravitational perturbation due to these planets, and, thereby, determine the
desired precession rate.
This is equivalent to averaging the interplanetary gravitational interactions
over the orbits of the other planets. It is reasonable to do this, since the precession period in question is
very much longer than the orbital period of any planet in the Solar System. Thus, by treating the other planets as
rings, we can calculate the mean gravitational perturbation due to these planets, and, thereby, determine the
desired precession rate.
![]() and the
and the ![]() , for
, for ![]() , be the planetary masses and orbital radii, respectively. Furthermore, let
, be the planetary masses and orbital radii, respectively. Furthermore, let ![]() be the mass of the Sun.
It follows, from the previous section, that the gravitational potential generated at the
be the mass of the Sun.
It follows, from the previous section, that the gravitational potential generated at the ![]() th planet by the Sun and
the other planets is
th planet by the Sun and
the other planets is
![$\displaystyle -\frac{G\,M_0}{R_i}-G \sum_{j< i}\frac{M_j}{R_i}\left[1+\frac{1}{...
...c{R_j}{R_i}\right)^2 + \frac{9}{64}\left(\frac{R_j}{R_i}\right)^4+\cdots\right]$](img2395.png)
![$\displaystyle -G \sum_{j> i}\frac{M_j}{R_j}\left[1+\frac{1}{4}\left(\frac{R_i}{R_j}\right)^2 + \frac{9}{64}\left(\frac{R_i}{R_j}\right)^4+\cdots\right].$](img2396.png)
![$\displaystyle -\frac{G\,M_0}{R_i^{\,2}}-\frac{G}{R_i^{\,2}} \sum_{j< i}M_j\left...
...R_j}{R_i}\right)^2
+ \frac{45}{64}\left(\frac{R_j}{R_i}\right)^4 +\cdots\right]$](img2399.png)
![$\displaystyle +\frac{G}{R_i^{\,2}} \sum_{j> i}M_j\,\left(\frac{R_i}{R_j}\right)...
...c{R_i}{R_j}\right)^2+ \frac{9}{16}\left(\frac{R_i}{R_j}\right)^4+\cdots\right].$](img2400.png)
![$\displaystyle \frac{2\,G\,M_0}{R_i^{\,2}}+\frac{G}{R_i^{\,2}} \sum_{j< i}M_j\le...
...R_j}{R_i}\right)^2
+ \frac{135}{32}\left(\frac{R_j}{R_i}\right)^4+\cdots\right]$](img2402.png)
![$\displaystyle + \frac{G}{R_i^{\,2}}\,\sum_{j> i}M_j\,\left(\frac{R_i}{R_j}\righ...
...{R_i}{R_j}\right)^2+ \frac{27}{16}\left(\frac{R_i}{R_j}\right)^4+\cdots\right],$](img2403.png)
![$\displaystyle \left[3 + \frac{R_i\,f'(R_i)}{f(R_i)}\right]^{-1/2} =1 + \frac{3}...
..._j}{R_i}\right)^2 + \frac{175}{64}\left(\frac{R_j}{R_i}
\right)^4+\cdots\right]$](img2405.png)
![$\displaystyle + \frac{3}{4}\sum_{j>i}\left(\frac{M_j}{M_0}\right)
\left(\frac{R...
...i}{R_j}\right)^2 + \frac{175}{64}\left(\frac{R_i}{R_j}
\right)^4+\cdots\right].$](img2406.png)
![$\displaystyle \pi\left\{1 + \frac{3}{4}\sum_{j<i}\left(\frac{M_j}{M_0}\right)
\...
...}\right)^2 + \frac{175}{64}\left(\frac{R_j}{R_i}
\right)^4+\cdots\right]\right.$](img2408.png)
![$\displaystyle \left.+ \frac{3}{4}\sum_{j>i}\left(\frac{M_j}{M_0}\right)
\left(\...
...right)^2 + \frac{175}{64}\left(\frac{R_i}{R_j}
\right)^4+\cdots\right]\right\}.$](img2409.png)
![$\displaystyle \frac{3\pi}{2}\sum_{j<i}\left(\frac{M_j}{M_0}\right)
\left(\frac{...
..._j}{R_i}\right)^2 + \frac{175}{64}\left(\frac{R_j}{R_i}
\right)^4+\cdots\right]$](img2411.png)
![$\displaystyle + \frac{3\pi}{2}\sum_{j>i}\left(\frac{M_j}{M_0}\right)
\left(\fra...
..._i}{R_j}\right)^2 + \frac{175}{64}\left(\frac{R_i}{R_j}
\right)^4+\cdots\right]$](img2412.png)

![]() ), which renders its perihelion point extremely sensitive to small perturbations.
), which renders its perihelion point extremely sensitive to small perturbations.