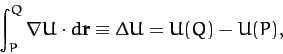Next: Newton's Third Law of
Up: Newton's Laws of Motion
Previous: Newton's First Law of
Newton's Second Law of Motion
Newton's second law of motion essentially states that if a point object
is subject to an external force, 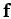 , then its equation of motion
is given by
, then its equation of motion
is given by
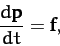 |
(13) |
where the momentum, 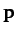 , is the product of the object's inertial
mass,
, is the product of the object's inertial
mass, 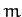 , and its velocity,
, and its velocity, 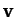 . If
. If 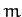 is not a function of time then the above expression reduces to the
familiar equation
is not a function of time then the above expression reduces to the
familiar equation
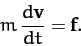 |
(14) |
Note that this equation is only valid in a inertial frame.
Clearly, the inertial mass of an object measures its reluctance to deviate
from its preferred state of uniform motion in a straight-line (in an
inertial frame). Of course, the above equation of motion can only be solved if we have an independent expression for the force, 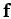 (i.e., a law of force).
Let us suppose that this is the case.
(i.e., a law of force).
Let us suppose that this is the case.
An important corollary of Newton's second law is that force is a vector
quantity. This must be the case, since the law equates force to the
product of a scalar (mass) and a vector (acceleration).
Note that acceleration is obviously a vector because it is directly related to displacement, which is the prototype of all vectors--see Appendix A. One consequence of force being a vector is
that two forces, 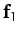 and
and 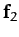 , both acting at a given
point, have the same effect as a single force,
, both acting at a given
point, have the same effect as a single force,
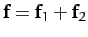 ,
acting at the same point, where the summation is performed according to the
laws of vector addition--see Appendix A. Likewise, a single force,
,
acting at the same point, where the summation is performed according to the
laws of vector addition--see Appendix A. Likewise, a single force, 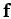 , acting at
a given point, has the same effect as two forces,
, acting at
a given point, has the same effect as two forces, 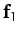 and
and 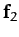 ,
acting at the same point, provided that
,
acting at the same point, provided that
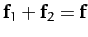 . This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in Newtonian dynamics.
. This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in Newtonian dynamics.
Taking the scalar product of Equation (14) with the velocity, 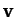 ,
we obtain
,
we obtain
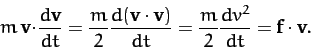 |
(15) |
This can be written
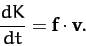 |
(16) |
where
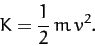 |
(17) |
The right-hand side of Equation (16) represents the rate at
which the force does work on the object: i.e.,
the rate at which the force transfers energy to the object. The quantity
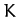 represents the energy the object possesses by virtue of its motion.
This type of energy is generally known as kinetic energy. Thus, Equation (16) states that any work done on point object by an external force
goes to increase the object's kinetic energy.
represents the energy the object possesses by virtue of its motion.
This type of energy is generally known as kinetic energy. Thus, Equation (16) states that any work done on point object by an external force
goes to increase the object's kinetic energy.
Suppose that, under the action of the force, 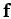 , our object moves
from point
, our object moves
from point 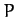 at time
at time 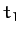 to point
to point 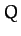 at time
at time 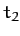 . The
net change in the object's kinetic energy is obtained by integrating
Equation (16):
. The
net change in the object's kinetic energy is obtained by integrating
Equation (16):
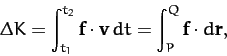 |
(18) |
since
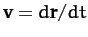 .
Here,
.
Here, 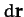 is an element of the object's path between points
is an element of the object's path between points 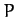 and
and 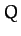 , and the integral in
, and the integral in 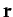 represents the net work done by the
force as the objects moves along the path from
represents the net work done by the
force as the objects moves along the path from 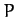 to
to 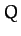 .
.
As described in Section A.15, there are basically two kinds
of forces in nature. Firstly, those for which line integrals of the type
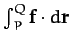 depend on the end points, but not
on the path taken between these points. Secondly, those for which
line integrals of the type
depend on the end points, but not
on the path taken between these points. Secondly, those for which
line integrals of the type
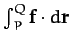 depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It was also
demonstrated in Section A.15 that if the line integral
depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It was also
demonstrated in Section A.15 that if the line integral
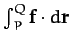 is path independent then the force
is path independent then the force 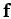 can always
be written as the gradient of a scalar field. In other words, all
conservative forces satisfy
can always
be written as the gradient of a scalar field. In other words, all
conservative forces satisfy
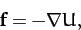 |
(19) |
for some scalar field 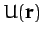 .
Note that
.
Note that
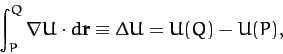 |
(20) |
irrespective of the path taken between 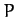 and
and 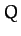 .
Hence, it follows from Equation (18)
that
.
Hence, it follows from Equation (18)
that
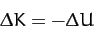 |
(21) |
for conservative forces. Another way of writing this is
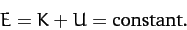 |
(22) |
Of course, we recognize this as an energy conservation equation: 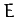 is the object's total energy, which is conserved;
is the object's total energy, which is conserved; 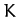 is the energy the
object has by virtue of its motion, otherwise know as its
kinetic energy; and
is the energy the
object has by virtue of its motion, otherwise know as its
kinetic energy; and 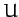 is the energy the object has by
virtue of its position, otherwise known as its potential
energy. Note, however, that we can only write such energy conservation
equations for conservative forces. Gravity is a good example of a conservative force.
Non-conservative forces, on the other hand, do not conserve energy. In general, this
is because of some sort of frictional energy loss which drains energy
from the dynamical system whilst it remains in motion.
Note that potential energy is undefined to an arbitrary additive constant.
In fact, it is only the difference in potential energy between
different points in space that is well-defined.
is the energy the object has by
virtue of its position, otherwise known as its potential
energy. Note, however, that we can only write such energy conservation
equations for conservative forces. Gravity is a good example of a conservative force.
Non-conservative forces, on the other hand, do not conserve energy. In general, this
is because of some sort of frictional energy loss which drains energy
from the dynamical system whilst it remains in motion.
Note that potential energy is undefined to an arbitrary additive constant.
In fact, it is only the difference in potential energy between
different points in space that is well-defined.



Next: Newton's Third Law of
Up: Newton's Laws of Motion
Previous: Newton's First Law of
Richard Fitzpatrick
2011-03-31
![]() and
and ![]() , both acting at a given
point, have the same effect as a single force,
, both acting at a given
point, have the same effect as a single force,
![]() ,
acting at the same point, where the summation is performed according to the
laws of vector addition--see Appendix A. Likewise, a single force,
,
acting at the same point, where the summation is performed according to the
laws of vector addition--see Appendix A. Likewise, a single force, ![]() , acting at
a given point, has the same effect as two forces,
, acting at
a given point, has the same effect as two forces, ![]() and
and ![]() ,
acting at the same point, provided that
,
acting at the same point, provided that
![]() . This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in Newtonian dynamics.
. This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in Newtonian dynamics.
![]() ,
we obtain
,
we obtain
![]() , our object moves
from point
, our object moves
from point ![]() at time
at time ![]() to point
to point ![]() at time
at time ![]() . The
net change in the object's kinetic energy is obtained by integrating
Equation (16):
. The
net change in the object's kinetic energy is obtained by integrating
Equation (16):
![]() depend on the end points, but not
on the path taken between these points. Secondly, those for which
line integrals of the type
depend on the end points, but not
on the path taken between these points. Secondly, those for which
line integrals of the type
![]() depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It was also
demonstrated in Section A.15 that if the line integral
depend
both on the end points, and the path taken between these points.
The first kind of force is termed conservative, whereas the
second kind is termed non-conservative. It was also
demonstrated in Section A.15 that if the line integral
![]() is path independent then the force
is path independent then the force ![]() can always
be written as the gradient of a scalar field. In other words, all
conservative forces satisfy
can always
be written as the gradient of a scalar field. In other words, all
conservative forces satisfy