


Next: Generalized Forces
Up: Lagrangian Dynamics
Previous: Introduction
Let the 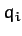 , for
, for 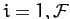 , be a set of coordinates which uniquely
specifies the instantaneous configuration of some dynamical system.
Here, it is assumed that each of the
, be a set of coordinates which uniquely
specifies the instantaneous configuration of some dynamical system.
Here, it is assumed that each of the 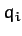 can vary independently.
The
can vary independently.
The 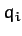 might be Cartesian coordinates, or polar
coordinates, or angles, or some mixture of all three types of coordinate, and are, therefore,
termed generalized coordinates. A dynamical system whose
instantaneous configuration is fully specified by
might be Cartesian coordinates, or polar
coordinates, or angles, or some mixture of all three types of coordinate, and are, therefore,
termed generalized coordinates. A dynamical system whose
instantaneous configuration is fully specified by 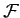 independent
generalized coordinates is said to have
independent
generalized coordinates is said to have 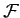 degrees of freedom.
For instance, the instantaneous position of a particle moving freely
in three dimensions is completely specified by its three Cartesian
coordinates,
degrees of freedom.
For instance, the instantaneous position of a particle moving freely
in three dimensions is completely specified by its three Cartesian
coordinates, 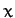 ,
, 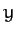 , and
, and 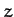 . Moreover, these coordinates are clearly
independent of one another.
Hence, a dynamical
system consisting of a single particle moving
freely in three dimensions has three degrees of freedom. If there are two freely moving
particles then the system has six degrees of freedom, and so on.
. Moreover, these coordinates are clearly
independent of one another.
Hence, a dynamical
system consisting of a single particle moving
freely in three dimensions has three degrees of freedom. If there are two freely moving
particles then the system has six degrees of freedom, and so on.
Suppose that we have a dynamical system consisting of  particles
moving freely in three dimensions. This is an
particles
moving freely in three dimensions. This is an
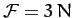 degree of
freedom system whose instantaneous configuration can be specified
by
degree of
freedom system whose instantaneous configuration can be specified
by 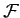 Cartesian coordinates. Let us denote these coordinates the
Cartesian coordinates. Let us denote these coordinates the
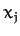 , for
, for 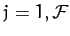 . Thus,
. Thus, 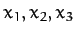 are the Cartesian coordinates
of the first particle,
are the Cartesian coordinates
of the first particle, 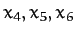 the Cartesian coordinates
of the second particle, etc. Suppose that the instantaneous configuration of the system can also be specified by
the Cartesian coordinates
of the second particle, etc. Suppose that the instantaneous configuration of the system can also be specified by 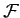 generalized
coordinates, which we shall denote the
generalized
coordinates, which we shall denote the 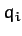 , for
, for 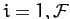 . Thus, the
. Thus, the
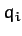 might be the spherical coordinates of the particles.
In general,
we expect the
might be the spherical coordinates of the particles.
In general,
we expect the 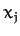 to be functions of the
to be functions of the 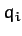 . In other words,
. In other words,
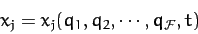 |
(592) |
for 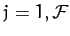 . Here, for the sake of generality, we have included the
possibility that the functional relationship between the
. Here, for the sake of generality, we have included the
possibility that the functional relationship between the 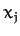 and the
and the
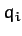 might depend on the time,
might depend on the time, 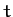 , explicitly. This would be the
case if the dynamical system were subject to time varying constraints. For
instance, a system consisting of a particle constrained to move on a surface which is itself
moving. Finally, by the chain rule, the variation of the
, explicitly. This would be the
case if the dynamical system were subject to time varying constraints. For
instance, a system consisting of a particle constrained to move on a surface which is itself
moving. Finally, by the chain rule, the variation of the 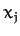 due to a variation of the
due to a variation of the 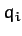 (at constant
(at constant 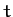 ) is given by
) is given by
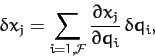 |
(593) |
for 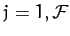 .
.



Next: Generalized Forces
Up: Lagrangian Dynamics
Previous: Introduction
Richard Fitzpatrick
2011-03-31
![]() particles
moving freely in three dimensions. This is an
particles
moving freely in three dimensions. This is an
![]() degree of
freedom system whose instantaneous configuration can be specified
by
degree of
freedom system whose instantaneous configuration can be specified
by ![]() Cartesian coordinates. Let us denote these coordinates the
Cartesian coordinates. Let us denote these coordinates the
![]() , for
, for ![]() . Thus,
. Thus, ![]() are the Cartesian coordinates
of the first particle,
are the Cartesian coordinates
of the first particle, ![]() the Cartesian coordinates
of the second particle, etc. Suppose that the instantaneous configuration of the system can also be specified by
the Cartesian coordinates
of the second particle, etc. Suppose that the instantaneous configuration of the system can also be specified by ![]() generalized
coordinates, which we shall denote the
generalized
coordinates, which we shall denote the ![]() , for
, for ![]() . Thus, the
. Thus, the
![]() might be the spherical coordinates of the particles.
In general,
we expect the
might be the spherical coordinates of the particles.
In general,
we expect the ![]() to be functions of the
to be functions of the ![]() . In other words,
. In other words,