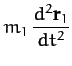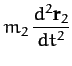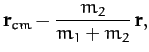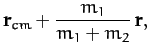Next: Binary Star Systems
Up: Two-Body Dynamics
Previous: Introduction
Reduced Mass
Suppose that our first object is of mass 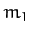 , and is located
at position vector
, and is located
at position vector 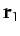 . Likewise, our second object
is of mass
. Likewise, our second object
is of mass 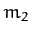 , and is located at position vector
, and is located at position vector 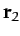 .
Let the first object exert a force
.
Let the first object exert a force 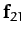 on the
second. By Newton's third law, the second object exerts an
equal and opposite force,
on the
second. By Newton's third law, the second object exerts an
equal and opposite force,
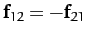 , on the
first. Suppose that there are no other forces in the problem. The equations of motion of our two objects are thus
, on the
first. Suppose that there are no other forces in the problem. The equations of motion of our two objects are thus
where
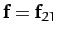 .
.
Now, the center of mass of our system is located at
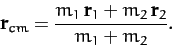 |
(324) |
Hence, we can write
where
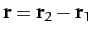 .
Substituting the above two equations into Equations (322) and (323),
and making use of the fact that the center of mass of an isolated system
does not accelerate (see Section 2.6), we find that both equations yield
.
Substituting the above two equations into Equations (322) and (323),
and making use of the fact that the center of mass of an isolated system
does not accelerate (see Section 2.6), we find that both equations yield
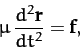 |
(327) |
where
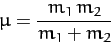 |
(328) |
is called the reduced mass. Hence, we have effectively converted our
original two-body problem into an equivalent one-body problem. In the equivalent problem, the
force 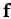 is the same as that acting on both objects in the original problem (modulo a minus sign). However, the mass,
is the same as that acting on both objects in the original problem (modulo a minus sign). However, the mass, 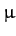 , is different, and
is less than either of
, is different, and
is less than either of 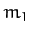 or
or 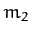 (which is why it is called the ``reduced'' mass).
(which is why it is called the ``reduced'' mass).



Next: Binary Star Systems
Up: Two-Body Dynamics
Previous: Introduction
Richard Fitzpatrick
2011-03-31