| (1089) |
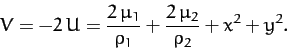 |
(1090) |
Let ![]() be the value of
be the value of ![]() at the
at the ![]() Lagrange point, for
Lagrange point, for ![]() . When
. When ![]() ,
it is easily demonstrated that
,
it is easily demonstrated that
| (1091) | |||
| (1092) | |||
| (1093) | |||
| (1094) | |||
| (1095) |
 |
 |
 |
 |
 |
Figures 50-54 show the intersection of the zero-velocity
surface ![]() with the
with the ![]() -
-![]() plane for various different values of
plane for various different values of ![]() , and
illustrate how the region from which
, and
illustrate how the region from which ![]() is dynamically excluded--which we shall term the excluded region--evolves as the value of
is dynamically excluded--which we shall term the excluded region--evolves as the value of
![]() is varied. Of course, any point not in the excluded region is in the so-called allowed region.
For
is varied. Of course, any point not in the excluded region is in the so-called allowed region.
For ![]() , the allowed region consists of two
separate oval regions centered on
, the allowed region consists of two
separate oval regions centered on ![]() and
and ![]() , respectively, plus an
outer region which lies beyond a
large circle centered on the origin. All three allowed regions are separated
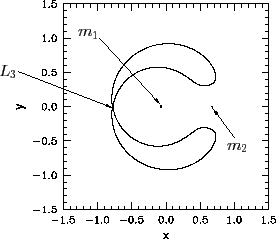
from one another by an excluded region--see Figure 50. When
, respectively, plus an
outer region which lies beyond a
large circle centered on the origin. All three allowed regions are separated
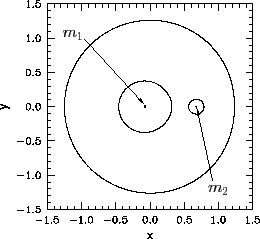
from one another by an excluded region--see Figure 50. When ![]() ,
the two inner allowed regions merge at the
,
the two inner allowed regions merge at the ![]() point--see Figure 51.
When
point--see Figure 51.
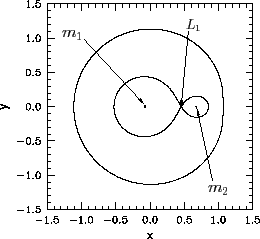
When ![]() , the inner and outer allowed regions merge at the
, the inner and outer allowed regions merge at the ![]() point, forming a horseshoe-like excluded region--see Figure 52.
When
point, forming a horseshoe-like excluded region--see Figure 52.
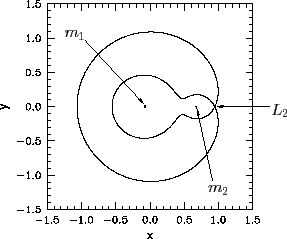
When ![]() , the excluded region splits in two at the
, the excluded region splits in two at the ![]() point--see Figure 53.
For
point--see Figure 53.
For ![]() , the two excluded regions are localized about the
, the two excluded regions are localized about the
![]() and
and
![]() points--see Figure 54. Finally, for
points--see Figure 54. Finally, for ![]() , there is no excluded
region.
, there is no excluded
region.
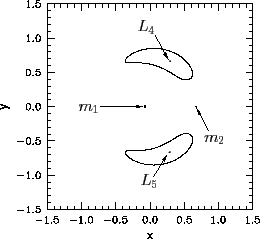
Figure 55 shows the zero-velocity surfaces and Lagrange points
calculated for the case ![]() . It can be seen that, at very small values of
. It can be seen that, at very small values of
![]() , the
, the ![]() and
and ![]() Lagrange points are almost equidistant from mass
Lagrange points are almost equidistant from mass ![]() .
Furthermore, mass
.
Furthermore, mass ![]() , and the
, and the ![]() ,
, ![]() , and
, and ![]() Lagrange points all lie approximately
on a unit circle,
centered on mass
Lagrange points all lie approximately
on a unit circle,
centered on mass ![]() . It follows that, when
. It follows that, when ![]() is small, the Lagrange points
is small, the Lagrange points ![]() ,
, ![]() and
and ![]() all
share the orbit of mass
all
share the orbit of mass ![]() about
about ![]() (in the inertial frame) with
(in the inertial frame) with ![]() being directly opposite
being directly opposite ![]() ,
,
![]() (by convention)
(by convention) ![]() ahead of
ahead of ![]() , and
, and ![]()
![]() behind.
behind.