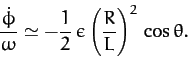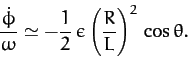Next: The Three-Body Problem
Up: Gravitational Potential Theory
Previous: Perihelion Precession of Mercury
- Show that
for a self-gravitating, rotating spheroid of ellipticity 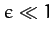 , mass
, mass
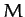 , mean radius
, mean radius  , and angular velocity
, and angular velocity  whose mass
density varies as
whose mass
density varies as 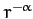 (where
(where 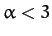 ). Demonstrate that the above formula matches
the observed rotational flattening of the Earth when
). Demonstrate that the above formula matches
the observed rotational flattening of the Earth when 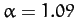 and
of Jupiter when
and
of Jupiter when  .
.
- The Moon's orbital period about the Earth is approximately 27.3 days,
and is in the same direction as the Earth's axial rotation (whose period is
24 hours). Use this data to show that high tides at a given point on the Earth
occur every 12 hours and 26 minutes.
- Estimate the tidal elongation of the Moon due to the Earth.
- Consider an artificial satellite in a circular orbit of radius
 about the Earth. Suppose that the normal to the plane of the orbit subtends
an angle
about the Earth. Suppose that the normal to the plane of the orbit subtends
an angle 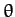 with the Earth's axis of rotation. By approximating the
orbiting satellite as a uniform ring, demonstrate that the Earth's oblateness causes
the plane of the satellite's orbit to precess about the Earth's rotational
axis at the rate
with the Earth's axis of rotation. By approximating the
orbiting satellite as a uniform ring, demonstrate that the Earth's oblateness causes
the plane of the satellite's orbit to precess about the Earth's rotational
axis at the rate
Here,  is the satellite's orbital angular velocity,
is the satellite's orbital angular velocity,
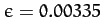 the Earth's ellipticity, and
the Earth's ellipticity, and 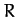 the Earth's radius. Note that the Earth's
axial moment of inertial is
the Earth's radius. Note that the Earth's
axial moment of inertial is
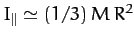 , where
, where
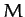 is the mass of the Earth.
is the mass of the Earth.
- A sun-synchronous satellite is one which always passes
over a given point on the Earth at the same local solar time. This is
achieved by fixing the precession rate of the satellite's orbital
plane such that it matches the rate at which the Sun appears to move
against the background of the stars. What orbital altitude above
the surface of the Earth would such a satellite need to have in order
to fly over all latitudes between
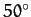 N and
N and 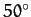 S? Is the
direction of the satellite orbit in the same sense as the Earth's rotation (prograde),
or the opposite sense (retrograde)?
S? Is the
direction of the satellite orbit in the same sense as the Earth's rotation (prograde),
or the opposite sense (retrograde)?



Next: The Three-Body Problem
Up: Gravitational Potential Theory
Previous: Perihelion Precession of Mercury
Richard Fitzpatrick
2011-03-31