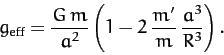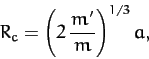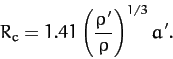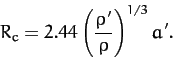Next: Precession and Forced Nutation
Up: Gravitational Potential Theory
Previous: Tidal Elongation
Roche Radius
Consider a spherical moon of mass 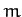 and radius
and radius 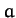 which is in a circular
orbit of radius
which is in a circular
orbit of radius 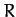 about a spherical planet of mass
about a spherical planet of mass 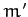 and radius
and radius 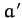 .
(Strictly speaking, the moon and the planet execute circular orbits about
their common center of mass. However, if the planet is much more massive
than the moon then the center of mass lies close to the
planet's center.) According to the analysis in the previous section, a constituent element of
the moon experiences a force per unit mass, due to the gravitational
field of the planet, which takes the form
.
(Strictly speaking, the moon and the planet execute circular orbits about
their common center of mass. However, if the planet is much more massive
than the moon then the center of mass lies close to the
planet's center.) According to the analysis in the previous section, a constituent element of
the moon experiences a force per unit mass, due to the gravitational
field of the planet, which takes the form
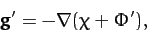 |
(948) |
where
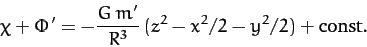 |
(949) |
Here, (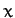 ,
, 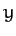 ,
, 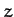 ) is a Cartesian coordinate system whose origin
is the center of the moon, and whose
) is a Cartesian coordinate system whose origin
is the center of the moon, and whose 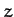 -axis always points toward the
center of the planet. It follows that
-axis always points toward the
center of the planet. It follows that
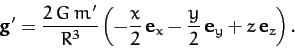 |
(950) |
This so-called tidal force is generated by the spatial variation of the
planet's gravitational field over the interior of the moon, and acts
to elongate the moon along an axis joining its center to that of the planet, and to compress it in any direction perpendicular
to this axis. Note that the magnitude of the tidal force increases strongly
as the radius, 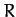 , of the moon's orbit decreases. Now, if the tidal
force becomes sufficiently strong then it can overcome the moon's self-gravity, and thereby rip the moon
apart. It follows that there is a minimum radius, generally referred to
as the Roche radius, at which a moon can orbit
a planet without being destroyed by tidal forces.
, of the moon's orbit decreases. Now, if the tidal
force becomes sufficiently strong then it can overcome the moon's self-gravity, and thereby rip the moon
apart. It follows that there is a minimum radius, generally referred to
as the Roche radius, at which a moon can orbit
a planet without being destroyed by tidal forces.
Let us derive an expression for the Roche radius. Consider a small mass
element at the point on the surface of the moon which lies closest to the planet, and at which the
tidal force is consequently largest (i.e., 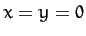 ,
, 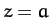 ). According to Equation (950), the
mass experiences an upward (from the moon's surface) tidal acceleration due to the gravitational attraction of the planet of the form
). According to Equation (950), the
mass experiences an upward (from the moon's surface) tidal acceleration due to the gravitational attraction of the planet of the form
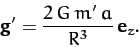 |
(951) |
The mass also experiences a downward gravitational acceleration due to the gravitational influence of the moon
which is written
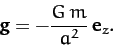 |
(952) |
Thus, the effective surface gravity at the point in question is
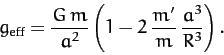 |
(953) |
Note that if 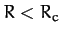 , where
, where
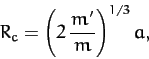 |
(954) |
then the effective gravity is negative. In other words, the
tidal force due to the planet is strong enough to overcome surface gravity and lift objects off the moon's surface.
If this is the case, and the tensile strength of the moon is negligible,
then it is fairly clear that the tidal force will start to break the moon apart. Hence, 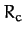 is the Roche radius. Now,
is the Roche radius. Now,
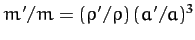 , where
, where 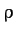 and
and 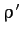 are the mean
mass densities of the moon and planet, respectively. Thus, the
above expression for the Roche radius can also be written
are the mean
mass densities of the moon and planet, respectively. Thus, the
above expression for the Roche radius can also be written
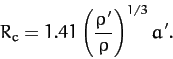 |
(955) |
The above calculation is somewhat inaccurate, since it fails to take into
account the inevitable distortion of the moon's shape in the presence of strong tidal
forces. (In fact, the calculation assumes that the moon
always remains spherical.) A more accurate calculation, which treats the moon
as a self-gravitating incompressible fluid, yields
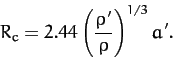 |
(956) |
It follows that if the planet and the moon have the same mean
density then the Roche radius is 2.44 times the planet's radius. Note that small orbital bodies such as rocks, or even
very small moons, can survive intact within the Roche radius because they
are held together by internal tensile forces rather than gravitational attraction.
However, this mechanism becomes progressively less effective as the size
of the body in question increases. Not surprisingly, virtually all large planetary moons
occurring in the Solar System have orbital radii which exceed the relevant Roche radius,
whereas virtually all planetary ring systems (which consist of myriads of small orbiting rocks)
have radii which
lie inside the relevant Roche radius.



Next: Precession and Forced Nutation
Up: Gravitational Potential Theory
Previous: Tidal Elongation
Richard Fitzpatrick
2011-03-31
![]() ,
, ![]() ). According to Equation (950), the
mass experiences an upward (from the moon's surface) tidal acceleration due to the gravitational attraction of the planet of the form
). According to Equation (950), the
mass experiences an upward (from the moon's surface) tidal acceleration due to the gravitational attraction of the planet of the form