


Next: Stokes Stream Function
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Introduction
A flow pattern is said to be axisymmetric when it is identical in every plane that passes through a
certain straight-line. The straight-line in question is referred to as the symmetry axis. Let us set up a Cartesian
coordinate system in which the symmetry axis corresponds to the  -axis. The flow is most
conveniently described in terms of the cylindrical coordinates (
-axis. The flow is most
conveniently described in terms of the cylindrical coordinates (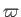 ,
, 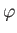 ,
,  ), or
the spherical coordinates (
), or
the spherical coordinates ( ,
,  ,
, 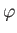 ). Here,
). Here,
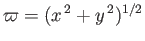 ,
,
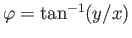 ,
,
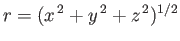 , and
, and
 . (See Appendix C.) In particular,
. (See Appendix C.) In particular,
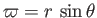 and
and
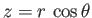 .
.
Richard Fitzpatrick
2016-03-31