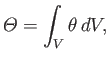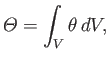Next: Mass Conservation
Up: Mathematical Models of Fluid
Previous: Viscosity
Suppose that
 is the density of some bulk fluid property (e.g., mass, momentum,
or energy) at position
is the density of some bulk fluid property (e.g., mass, momentum,
or energy) at position  and time
and time 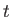 . In other words, suppose that, at time
. In other words, suppose that, at time 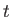 , an infinitesimal fluid element of volume
, an infinitesimal fluid element of volume  , located
at position
, located
at position  , contains an amount
, contains an amount
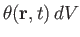 of the property in question. Note, incidentally,
that
of the property in question. Note, incidentally,
that  can be either a scalar, a component of a vector, or even a component of a tensor.
The total
amount of the property contained within some fixed volume
can be either a scalar, a component of a vector, or even a component of a tensor.
The total
amount of the property contained within some fixed volume  is
is
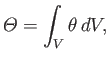 |
(1.28) |
where the integral is taken over all elements of  . Let
. Let 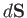 be an outward directed
element of the bounding surface of
be an outward directed
element of the bounding surface of  . Suppose that this element is located at point
. Suppose that this element is located at point  . The volume of fluid that
flows per second across the element, and so out of
. The volume of fluid that
flows per second across the element, and so out of  , is
, is
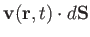 . Thus, the
amount of the fluid property under consideration that is convected across the element per second is
. Thus, the
amount of the fluid property under consideration that is convected across the element per second is
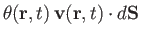 . It follows that the net amount of the property that
is convected out of volume
. It follows that the net amount of the property that
is convected out of volume  by fluid flow across its bounding surface
by fluid flow across its bounding surface  is
is
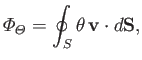 |
(1.29) |
where the integral is taken over all outward directed elements of  . Suppose, finally, that
the property in question is created within the volume
. Suppose, finally, that
the property in question is created within the volume  at the rate
at the rate
 per second.
The conservation equation for the fluid property takes the form
per second.
The conservation equation for the fluid property takes the form
 |
(1.30) |
In other words, the rate of increase in the amount of the property contained within  is the
difference between the creation rate of the property inside
is the
difference between the creation rate of the property inside  , and the rate at
which the property is convected out of
, and the rate at
which the property is convected out of  by fluid flow.
The previous conservation law can also be written
by fluid flow.
The previous conservation law can also be written
 |
(1.31) |
Here,
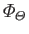 is termed the flux of the property out of
is termed the flux of the property out of  , whereas
, whereas
 is called the net generation rate of the property within
is called the net generation rate of the property within  .
.



Next: Mass Conservation
Up: Mathematical Models of Fluid
Previous: Viscosity
Richard Fitzpatrick
2016-03-31