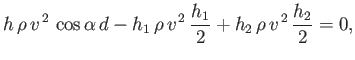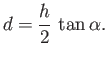Next: Exercises
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Inviscid Flow Over a
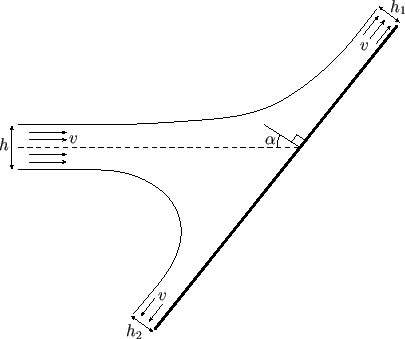
Consider a two-dimensional jet of width 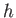 and uniform speed
and uniform speed 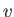 that impinges on a rigid plate,
at an angle
that impinges on a rigid plate,
at an angle 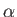 to the normal to the plate, and divides into two
streams, running along the plate, whose widths are ultimately uniform, and equal to
to the normal to the plate, and divides into two
streams, running along the plate, whose widths are ultimately uniform, and equal to 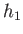 and
and 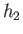 . (See Figure 5.14.)
We expect the pressure well upstream of the plate to be atmospheric all the way across the jet, because the jet is not yet decelerating. Likewise, we expect the pressure well downstream of the strike point to be atmospheric all the way across the two streams that run along the plate, because the streams are no longer accelerating (and, hence, their
widths are constant). It immediately follows from Bernoulli's theorem that the asymptotic flow speed in the
two streams is
. (See Figure 5.14.)
We expect the pressure well upstream of the plate to be atmospheric all the way across the jet, because the jet is not yet decelerating. Likewise, we expect the pressure well downstream of the strike point to be atmospheric all the way across the two streams that run along the plate, because the streams are no longer accelerating (and, hence, their
widths are constant). It immediately follows from Bernoulli's theorem that the asymptotic flow speed in the
two streams is 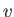 , as indicated in Figure 5.14.
, as indicated in Figure 5.14.
Figure 5.14:
A two-dimensional jet impinging on a rigid plate.
 |
Fluid continuity demands that
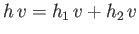 , or
, or
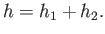 |
(5.134) |
Moreover, because the plate can only exert a normal force on the fluid, it follows that the parallel (to the plate) momentum
flux of the incident jet must equal the net parallel momentum flux of the two streams. In other words,
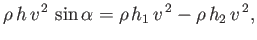 |
(5.135) |
or
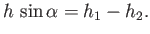 |
(5.136) |
Equations (5.134) and (5.136) can be combined to give
Figure 5.15:
Determination of the center of pressure.
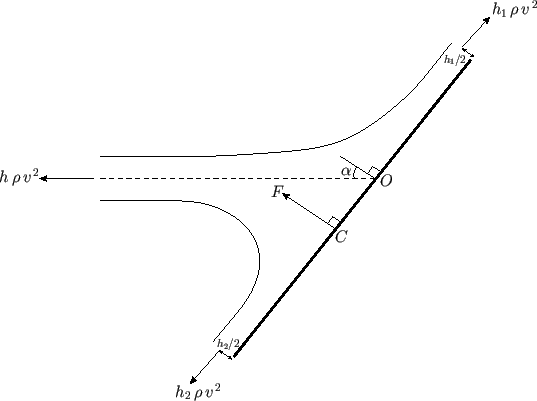 |
Let us apply the Euler momentum theorem (see Section 4.4) to the flux tube shown
in Figure 5.14, treating the plate as one of the walls of the tube. By symmetry, the net force (per unit width perpendicular to the page) exerted across the walls and ends of the tube
is the resultant of the three forces shown in Figure 5.15. It is easily demonstrated that this net
force, 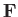 , is normal to the plate, as shown in the figure, and of magnitude
, is normal to the plate, as shown in the figure, and of magnitude
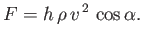 |
(5.139) |
Obviously, the force in question corresponds to the force exerted by the plate on the fluid. An equal and opposite force is
exerted by the fluid on the plate. (Note that there is no net pressure force on the flux tube because it is
entirely surrounded by fluid at the same pressure: i.e., atmospheric pressure.) The line of action of the resultant force passes through the
so-called center of pressure, 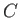 . This is displaced slightly from the point,
. This is displaced slightly from the point, 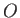 , where the
middle of the jet strikes the plate. (See Figure 5.15.) Let
, where the
middle of the jet strikes the plate. (See Figure 5.15.) Let 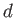 be the distance
be the distance 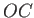 . We can calculate
. We can calculate 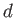 by demanding that
the net moment of the three forces shown in Figure 5.15 about point
by demanding that
the net moment of the three forces shown in Figure 5.15 about point 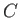 be zero. In other
words,
be zero. In other
words,
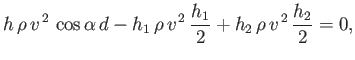 |
(5.140) |
which yields
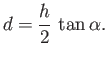 |
(5.141) |



Next: Exercises
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Inviscid Flow Over a
Richard Fitzpatrick
2016-03-31

![]() , or
, or
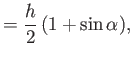
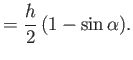
![]() , is normal to the plate, as shown in the figure, and of magnitude
, is normal to the plate, as shown in the figure, and of magnitude