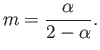Next: Inviscid Flow Over a
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Motion of a Submerged
Inviscid Flow Past a Semi-Infinite Wedge
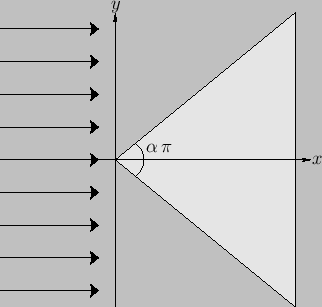
Consider the situation, illustrated in Figure 5.10, in which incompressible irrotational flow is incident on a
impenetrable rigid wedge whose apex subtends an angle
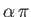 . Let the cross-section of the wedge in the
. Let the cross-section of the wedge in the  -
- plane
be both
plane
be both  -independent and symmetric about the
-independent and symmetric about the  -axis. Furthermore, let the apex of
the wedge lie at
-axis. Furthermore, let the apex of
the wedge lie at  . Finally, let the upstream flow a large distance from the
wedge be parallel to the
. Finally, let the upstream flow a large distance from the
wedge be parallel to the  -axis.
-axis.
Figure 5.10:
Inviscid flow past a wedge.
 |
Because the flow is two-dimensional, incompressible, and irrotational, it can be represented in terms of a stream function that
satisfies Laplace's equation. Moreover, in cylindrical coordinates, this equation takes the form (5.61). The
boundary conditions on the stream function are
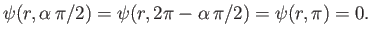 |
(5.126) |
The first two boundary conditions ensure that the normal velocity at the surface of the wedge is zero. The third boundary condition
follows from the observation that, by symmetry, the streamline that meets the apex of the wedge splits in two, and then flows along its
top and bottom boundaries, combined with the well-known result that 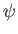 is constant on a streamline.
It is easily demonstrated that
is constant on a streamline.
It is easily demonstrated that
![$\displaystyle \psi(r,\theta) = \frac{A}{1+m}\,r^{\,1+m}\,\sin\left[(1+m)\,(\pi-\theta)\right]$](img1870.png) |
(5.127) |
is a solution of Equation (5.61). Moreover, this solution satisfies the boundary conditions provided
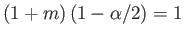 , or
, or
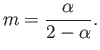 |
(5.128) |
Because, as is well known, the solutions to Laplace's equation (for problems with well-posed boundary conditions) are
unique (Riley 1974), we can be sure that Equation (5.127) is the correct
solution to the problem under investigation. According to this solution, the tangential velocity on the surface of the
wedge is given by
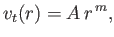 |
(5.129) |
where 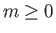 .
Note that the tangential velocity is zero at the apex of the wedge. Because the normal velocity is also zero at this point, we
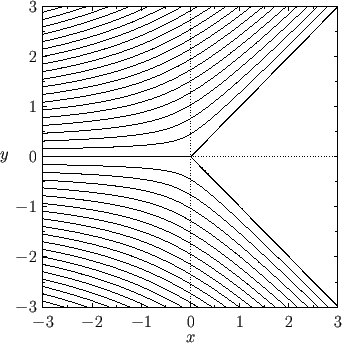
conclude that the apex is a stagnation point of the flow. Figure 5.11 shows the streamlines of the
flow for the case
.
Note that the tangential velocity is zero at the apex of the wedge. Because the normal velocity is also zero at this point, we
conclude that the apex is a stagnation point of the flow. Figure 5.11 shows the streamlines of the
flow for the case
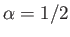 .
.
Figure:
Streamlines of inviscid incompressible irrotational flow past a 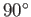 wedge.
wedge.
 |



Next: Inviscid Flow Over a
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Motion of a Submerged
Richard Fitzpatrick
2016-03-31