 |
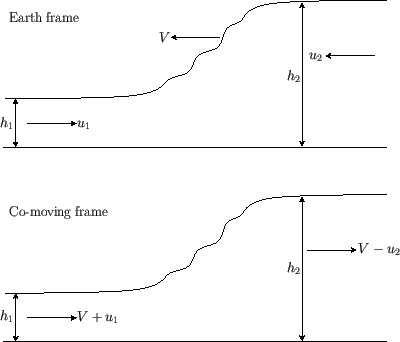
A tidal bore is a sort of hydraulic jump that propagates up (i.e., upstream) a river estuary. The upper part of Figure 4.7 shows such a bore in the
local rest frame of the Earth. The bore is propagating at the velocity ![]() up a river of uniform width, and depth
up a river of uniform width, and depth ![]() , that is flowing downstream at
the velocity
, that is flowing downstream at
the velocity ![]() . The flow behind the bore is of depth
. The flow behind the bore is of depth ![]() , and is flowing upstream at the velocity
, and is flowing upstream at the velocity ![]() . The lower part of the figure shows
the same phenomenon in the rest frame of the bore. In this frame, we observe a stationary hydraulic jump with an upstream depth and flow
velocity
. The lower part of the figure shows
the same phenomenon in the rest frame of the bore. In this frame, we observe a stationary hydraulic jump with an upstream depth and flow
velocity ![]() and
and ![]() , respectively, and a downstream depth and flow velocity
, respectively, and a downstream depth and flow velocity ![]() and
and ![]() , respectively.
Making use of Equations (4.44) and (4.45), we obtain
, respectively.
Making use of Equations (4.44) and (4.45), we obtain
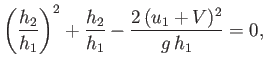 |
(4.62) |
![$\displaystyle V = -u_1 +\left[\frac{g\,h_2\,(h_1+h_2)}{2\,h_1}\right]^{1/2}.$](img1516.png) |
(4.63) |
Tidal bores are found in river estuaries where a funneling effect causes the speed of the incoming tide to increase to such a point that the flow becomes super-critical. For example, bores can be observed daily on the River Severn in England.