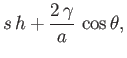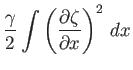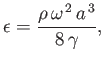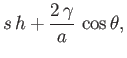Next: Incompressible Inviscid Flow
Up: Surface Tension
Previous: Axisymmetric Soap-Bubbles
- Show that if
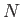 equal spheres of water coalesce so as to form a single spherical drop then the
surface energy is decreased by a factor
equal spheres of water coalesce so as to form a single spherical drop then the
surface energy is decreased by a factor
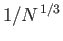 . (Lamb 1928.)
. (Lamb 1928.)
- A circular cylinder of radius
 , height
, height 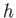 , and specific gravity
, and specific gravity 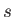 floats upright in water. Show
that the depth of the base below the general level of the water surface is
floats upright in water. Show
that the depth of the base below the general level of the water surface is
where 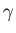 is the surface tension at the air/water interface, and
is the surface tension at the air/water interface, and  the contact angle of the
interface with the cylinder. (Lamb 1928.)
the contact angle of the
interface with the cylinder. (Lamb 1928.)
- A film of water is held between two parallel plates of glass a small distance
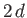 apart. Prove
that the apparent attraction between the plates is
apart. Prove
that the apparent attraction between the plates is
where 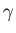 is the surface tension at the air/water interface,
is the surface tension at the air/water interface,  the angle of contact of the
interface with glass,
the angle of contact of the
interface with glass,  the area of the film, and
the area of the film, and  the circumference of the film. (Lamb 1928.)
the circumference of the film. (Lamb 1928.)
- Show that if the surface of a sheet of water is slightly corrugated then the surface energy is
increased by
per unit breadth of the corrugations. Here,  is measured horizontally, perpendicular to the corrugations.
Moreover,
is measured horizontally, perpendicular to the corrugations.
Moreover, 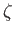 denotes the elevation of the surface above the mean level. Finally,
denotes the elevation of the surface above the mean level. Finally, 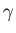 is the
surface tension at an air/water interface. If the corrugations are sinusoidal, such that
is the
surface tension at an air/water interface. If the corrugations are sinusoidal, such that
show that the average increment of the surface energy per unit area is
(Lamb 1928.)
- A mass of liquid, which is held together by surface tension alone, revolves about a
fixed axis at a small angular velocity
 , so as to assume a slightly spheroidal shape of
mean radius
, so as to assume a slightly spheroidal shape of
mean radius  . Prove that the ellipticity of the spheroid is
. Prove that the ellipticity of the spheroid is
where  is the uniform mass density, and
is the uniform mass density, and 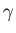 the surface tension. [If
the surface tension. [If  is the maximum radius, and
is the maximum radius, and 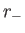 the minimum radius, then
the minimum radius, then
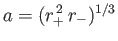 , and
the ellipticity is defined
, and
the ellipticity is defined
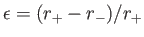 .] (Lamb 1928.)
.] (Lamb 1928.)
- A liquid mass rotates, in the form of a circular ring of radius
 and small cross-section, with a constant angular
velocity
and small cross-section, with a constant angular
velocity  , about an axis normal to the plane of the ring, and passing through its center. The mass is
held together by surface tension alone. Show that the section of the ring must be approximately circular.
Demonstrate that
, about an axis normal to the plane of the ring, and passing through its center. The mass is
held together by surface tension alone. Show that the section of the ring must be approximately circular.
Demonstrate that
where  is the density,
is the density, 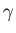 the surface tension, and
the surface tension, and 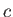 the radius of the cross-section. (Lamb 1928.)
the radius of the cross-section. (Lamb 1928.)
- Two spherical soap bubbles of radii
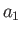 and
and 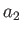 are made to coalesce. Show that when the
temperature of the gas in the resulting bubble has returned to its initial value the radius
are made to coalesce. Show that when the
temperature of the gas in the resulting bubble has returned to its initial value the radius  of
the bubble satisfies
of
the bubble satisfies
where 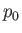 is the ambient pressure, and
is the ambient pressure, and 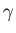 the surface tension of the soap/air interfaces. (Batchelor 2000.)
the surface tension of the soap/air interfaces. (Batchelor 2000.)
- A rigid sphere of radius
 rests on a flat rigid surface, and a small amount of liquid surrounds
the contact point, making a concave-planar lens whose diameter is small compared to
rests on a flat rigid surface, and a small amount of liquid surrounds
the contact point, making a concave-planar lens whose diameter is small compared to  . The
angle of contact of the liquid/air interface with each of the solid surfaces is zero, and the surface tension of the interface is
. The
angle of contact of the liquid/air interface with each of the solid surfaces is zero, and the surface tension of the interface is 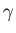 . Show that there is an adhesive force of magnitude
. Show that there is an adhesive force of magnitude
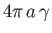 acting
on the sphere. (It is interesting to note that the force is independent of the volume of liquid.) (Batchelor 2000.)
acting
on the sphere. (It is interesting to note that the force is independent of the volume of liquid.) (Batchelor 2000.)
- Two small solid bodies are floating on the surface of a liquid. Show that the effect of
surface tension is to make the objects approach one another if the liquid/air interface has either an acute or an obtuse angle
of contact with both bodies, and to make them move away from one another if the interface has an acute
angle of contact with one body, and an obtuse angle of contact with the other. (Batchelor 2000.)



Next: Incompressible Inviscid Flow
Up: Surface Tension
Previous: Axisymmetric Soap-Bubbles
Richard Fitzpatrick
2016-03-31