


Next: Ellipsoidal Potential Theory
Up: Non-Cartesian Coordinates
Previous: Spherical Coordinates
- Find the Cartesian components of the basis vectors
 ,
,
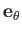 , and
, and  of the cylindrical coordinate
system. Verify that the vectors are mutually orthogonal. Do the
same for the basis vectors
of the cylindrical coordinate
system. Verify that the vectors are mutually orthogonal. Do the
same for the basis vectors  ,
,
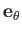 , and
, and
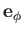 of the spherical coordinate system.
of the spherical coordinate system.
- Use cylindrical coordinates to prove that the volume of a right cylinder of radius
 and
length
and
length 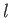 is
is
 . Demonstrate that the moment of inertia of a uniform cylinder of mass
. Demonstrate that the moment of inertia of a uniform cylinder of mass 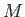 and radius
and radius  about
its symmetry axis is
about
its symmetry axis is
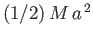 .
.
- Use spherical coordinates to prove that the volume of a sphere of radius
 is
is
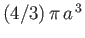 . Demonstrate that the moment of inertia of a uniform sphere of mass
. Demonstrate that the moment of inertia of a uniform sphere of mass 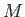 and radius
and radius  about
an axis passing through its center is
about
an axis passing through its center is
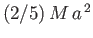 .
.
- For what value(s) of
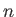 is
is
 , where
, where  is a
spherical coordinate?
is a
spherical coordinate?
- For what value(s) of
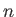 is
is
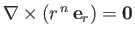 , where
, where  is a
spherical coordinate?
is a
spherical coordinate?
- Find a vector field
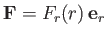 satisfying
satisfying
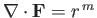 for
for 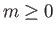 . Here,
. Here,
 is a spherical coordinate.
is a spherical coordinate.
- Use the divergence theorem to show that
where  is a volume enclosed by a surface
is a volume enclosed by a surface  .
.
- Use the previous result (for
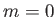 ) to demonstrate that the volume of a right cone is
one third the volume of the right cylinder having the same base and height.
) to demonstrate that the volume of a right cone is
one third the volume of the right cylinder having the same base and height.
- The electric field generated by a
 -directed electric dipole of moment
-directed electric dipole of moment  , located
at the origin, is
, located
at the origin, is
where
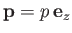 , and
, and  is a spherical coordinate. Find the components of
is a spherical coordinate. Find the components of
 in
the spherical coordinate system. Calculate
in
the spherical coordinate system. Calculate
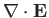 and
and
 .
.
- Show that the parabolic cylindrical coordinates
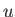 ,
, 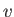 ,
,  , defined
by the equations
, defined
by the equations
 ,
, 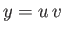 ,
,  , where
, where  ,
,  ,
,  are Cartesian
coordinates, are orthogonal. Find the scale factors
are Cartesian
coordinates, are orthogonal. Find the scale factors  ,
, 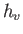 ,
, 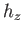 .
What shapes are the
.
What shapes are the
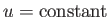 and
and
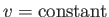 surfaces?
Write an expression for
surfaces?
Write an expression for
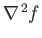 in parabolic cylindrical coordinates.
in parabolic cylindrical coordinates.
- Show that the elliptic cylindrical coordinates
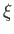 ,
,  ,
,  , defined
by the equations
, defined
by the equations
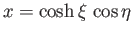 ,
,
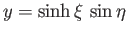 ,
,  , where
, where  ,
,  ,
,  are Cartesian
coordinates, and
are Cartesian
coordinates, and
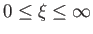 ,
,
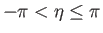 , are orthogonal. Find the scale factors
, are orthogonal. Find the scale factors  ,
, 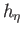 ,
, 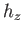 .
What shapes are the
.
What shapes are the
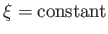 and
and
 surfaces?
Write an expression for
surfaces?
Write an expression for 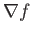 in elliptical cylindrical coordinates.
in elliptical cylindrical coordinates.



Next: Ellipsoidal Potential Theory
Up: Non-Cartesian Coordinates
Previous: Spherical Coordinates
Richard Fitzpatrick
2016-03-31
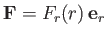 satisfying
satisfying
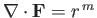 for
for 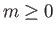 . Here,
. Here,
 is a spherical coordinate.
is a spherical coordinate.
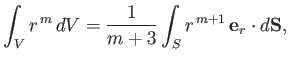
 is a volume enclosed by a surface
is a volume enclosed by a surface  .
.
 ) to demonstrate that the volume of a right cone is
one third the volume of the right cylinder having the same base and height.
) to demonstrate that the volume of a right cone is
one third the volume of the right cylinder having the same base and height.
![$\displaystyle {\bf E}({\bf r})= \frac{1}{4\pi\,\epsilon_0} \left[\frac{3\,({\bf e}_r\cdot {\bf p})\,{\bf e}_r-{\bf p}}{r^3}\right],
$](img7208.png)