


Next: Non-Cartesian Coordinates
Up: Cartesian Tensors
Previous: Isotropic Tensors
- Show that a general second-order tensor
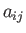 can be decomposed into three tensors
can be decomposed into three tensors
where 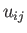 is symmetric (i.e.,
is symmetric (i.e.,
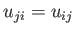 ) and traceless (i.e.,
) and traceless (i.e., 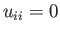 ),
), 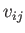 is isotropic,
and
is isotropic,
and 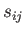 only has three independent components.
only has three independent components.
- Use tensor methods to establish the following vector identities:
-
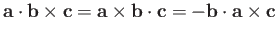 .
.
-
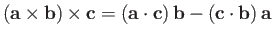 .
.
-
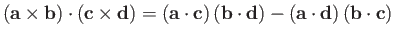 .
.
-
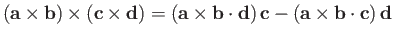 .
.
-
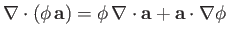 .
.
-
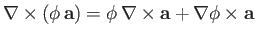 .
.
-
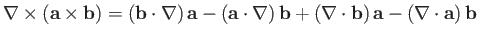 .
.
-
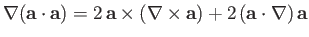 .
.
-
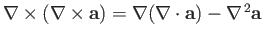 .
.
Here,
![$ [({\bf b}\cdot{\nabla}){\bf a}]_i= b_j\,\partial a_i/\partial x_j$](img6992.png) , and
, and
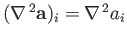 .
.
- A quadric surface has an equation of the form
Show that the coefficients in the previous expression transform under rotation of
the coordinate axes like the components of a symmetric second-order tensor. Hence, demonstrate that the equation for the surface can be written in the form
where the 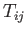 are the components of the aforementioned tensor.
are the components of the aforementioned tensor.
- The determinant of a second-order tensor
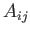 is defined
is defined
- Show that
is an alternative, and entirely equivalent, definition.
- Demonstrate that
 is invariant under rotation of the coordinate axes.
is invariant under rotation of the coordinate axes.
- Suppose that
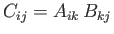 . Show that
. Show that
- If
then 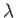 and
and 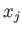 are said to be eigenvalues and eigenvectors of the second-order tensor
are said to be eigenvalues and eigenvectors of the second-order tensor 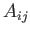 , respectively.
The eigenvalues of
, respectively.
The eigenvalues of 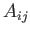 are calculated by solving the related homogeneous matrix equation
are calculated by solving the related homogeneous matrix equation
Now, it is a standard result in linear algebra that an equation of the previous form only has a non-trivial
solution when (Riley 1974)
Demonstrate that the eigenvalues of 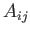 satisfy the cubic polynomial
satisfy the cubic polynomial
where
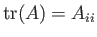 and
and
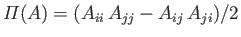 .
Hence, deduce that
.
Hence, deduce that 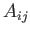 possesses three eigenvalues--
possesses three eigenvalues--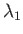 ,
, 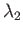 , and
, and 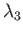 (say).
Moreover, show that
(say).
Moreover, show that
- Suppose that
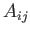 is a (real) symmetric second-order tensor: that is,
is a (real) symmetric second-order tensor: that is,
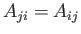 .
.
- Demonstrate that the eigenvalues of
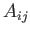 are all real, and that the eigenvectors
can be chosen to be real.
are all real, and that the eigenvectors
can be chosen to be real.
- Show that eigenvectors of
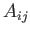 corresponding to different eigenvalues
are orthogonal to one another. Hence, deduce that the three eigenvectors of
corresponding to different eigenvalues
are orthogonal to one another. Hence, deduce that the three eigenvectors of 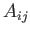 are, or can be chosen to be, mutually orthogonal.
are, or can be chosen to be, mutually orthogonal.
- Demonstrate that
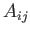 takes the diagonal form
takes the diagonal form
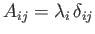 (no sum) in a
Cartesian coordinate system in which the coordinate axes are each parallel to one of the eigenvectors.
(no sum) in a
Cartesian coordinate system in which the coordinate axes are each parallel to one of the eigenvectors.
- In an isotropic elastic medium under stress, the displacement
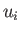 satisfies
satisfies
where
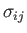 is the stress tensor (note that
is the stress tensor (note that
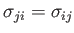 ),
),  the mass density
(which is a uniform constant), and
the mass density
(which is a uniform constant), and
the isotropic stiffness tensor.
Here, 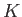 and
and 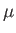 are the bulk modulus and shear modulus of the medium, respectively.
Show that the divergence and the curl of
are the bulk modulus and shear modulus of the medium, respectively.
Show that the divergence and the curl of 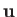 both satisfy wave equations. Furthermore, demonstrate that
the characteristic wave velocities of the divergence and curl waves are
both satisfy wave equations. Furthermore, demonstrate that
the characteristic wave velocities of the divergence and curl waves are
![$ [(K+4\mu/3)/\rho]^{1/2}$](img7024.png) and
and
 , respectively.
, respectively.



Next: Non-Cartesian Coordinates
Up: Cartesian Tensors
Previous: Isotropic Tensors
Richard Fitzpatrick
2016-03-31
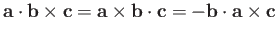 .
.
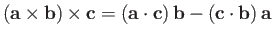 .
.
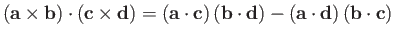 .
.
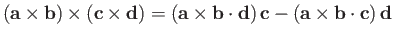 .
.
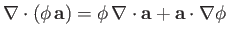 .
.
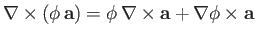 .
.
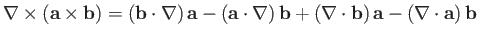 .
.
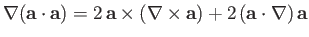 .
.
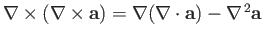 .
.
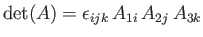
 is invariant under rotation of the coordinate axes.
is invariant under rotation of the coordinate axes.
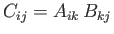 . Show that
. Show that
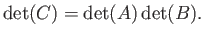
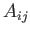 are all real, and that the eigenvectors
can be chosen to be real.
are all real, and that the eigenvectors
can be chosen to be real.
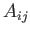 corresponding to different eigenvalues
are orthogonal to one another. Hence, deduce that the three eigenvectors of
corresponding to different eigenvalues
are orthogonal to one another. Hence, deduce that the three eigenvectors of 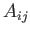 are, or can be chosen to be, mutually orthogonal.
are, or can be chosen to be, mutually orthogonal.
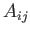 takes the diagonal form
takes the diagonal form
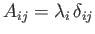 (no sum) in a
Cartesian coordinate system in which the coordinate axes are each parallel to one of the eigenvectors.
(no sum) in a
Cartesian coordinate system in which the coordinate axes are each parallel to one of the eigenvectors.

