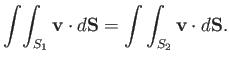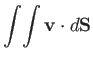Next: Volume Integrals
Up: Vectors and Vector Fields
Previous: Surface Integrals
Surface integrals often occur during vector analysis. For instance, the rate of
flow of a liquid of velocity 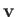 through an infinitesimal
surface of vector area
through an infinitesimal
surface of vector area 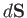 is
is
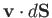 . The net rate of flow through a surface
. The net rate of flow through a surface 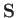 made up
of
very many infinitesimal surfaces is
made up
of
very many infinitesimal surfaces is
![$\displaystyle \int\!\int_S {\bf v}\cdot d{\bf S} = \lim_{dS\rightarrow 0}\left[ \sum v\,\cos\theta \,dS\right],$](img6500.png) |
(A.95) |
where  is the angle subtended between the normal to the surface and the
flow velocity.
is the angle subtended between the normal to the surface and the
flow velocity.
Analogously to line integrals, most
surface integrals depend both on the surface and the rim.
But some (very important) integrals depend only on the rim, and not on the nature
of the surface which spans it. As an example of this, consider incompressible fluid
flow between two surfaces 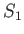 and
and 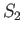 that end on the same rim. (See Figure A.23.)
The volume between the surfaces is constant, so what goes in must come out, and
that end on the same rim. (See Figure A.23.)
The volume between the surfaces is constant, so what goes in must come out, and
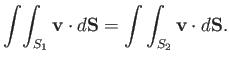 |
(A.96) |
It follows that
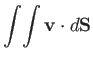 |
(A.97) |
depends only on the rim, and not on the form of surfaces 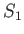 and
and 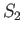 .
.



Next: Volume Integrals
Up: Vectors and Vector Fields
Previous: Surface Integrals
Richard Fitzpatrick
2016-03-31
![$\displaystyle \int\!\int_S {\bf v}\cdot d{\bf S} = \lim_{dS\rightarrow 0}\left[ \sum v\,\cos\theta \,dS\right],$](img6500.png)
![$\displaystyle \int\!\int_S {\bf v}\cdot d{\bf S} = \lim_{dS\rightarrow 0}\left[ \sum v\,\cos\theta \,dS\right],$](img6500.png)
![]() and
and ![]() that end on the same rim. (See Figure A.23.)
The volume between the surfaces is constant, so what goes in must come out, and
that end on the same rim. (See Figure A.23.)
The volume between the surfaces is constant, so what goes in must come out, and