


Next: Surface Integrals
Up: Vectors and Vector Fields
Previous: Line Integrals
Vector Line Integrals
A vector field is defined as a set of vectors associated with each point in space.
For instance, the velocity
 in a moving liquid
(e.g., a whirlpool) constitutes
a vector field. By analogy, a scalar field is a set of scalars associated with each
point in space. An example of a scalar field is the temperature distribution
in a moving liquid
(e.g., a whirlpool) constitutes
a vector field. By analogy, a scalar field is a set of scalars associated with each
point in space. An example of a scalar field is the temperature distribution
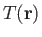 in
a furnace.
in
a furnace.
Consider a general vector field
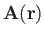 . Let
. Let
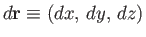 be the
vector element of line length. Vector line integrals often arise as
be the
vector element of line length. Vector line integrals often arise as
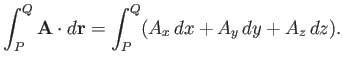 |
(A.81) |
For instance, if 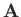 is a force-field then the line integral is the work done in going from
is a force-field then the line integral is the work done in going from
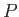 to
to  .
.
For example, consider the work done by a repulsive inverse-square
central field,
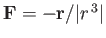 . The
element of work done is
. The
element of work done is
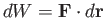 .
Take
.
Take
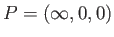 and
and 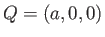 . The first route considered is along the
. The first route considered is along the  -axis, so
-axis, so
![$\displaystyle W = \int_{\infty}^a \left(-\frac{1}{x^{\,2}}\right)\,dx = \left[\frac{1}{x}\right]_{\infty}^a =\frac{1}{a}.$](img6481.png) |
(A.82) |
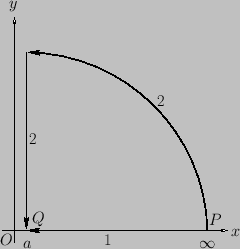
The second route is, firstly, around a large circle (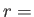 constant) to the point
(
constant) to the point
( ,
, 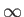 , 0), and then parallel to the
, 0), and then parallel to the  -axis. (See Figure A.16). In the first part, no work is
done,
because
-axis. (See Figure A.16). In the first part, no work is
done,
because 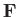 is perpendicular to
is perpendicular to 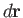 . In the second part,
. In the second part,
![$\displaystyle W = \int_{\infty}^0 \frac{-y\,dy}{(a^{\,2} + y^{\,2})^{3/2}} = \left[\frac{1}{(y^{\,2}+a^{\,2})^{1/2}} \right]^0_\infty = \frac{1}{a}.$](img6482.png) |
(A.83) |
In this case, the integral is independent of the path. However, not all vector line integrals
are path independent.
Figure A.16:
An example vector line integral.
 |



Next: Surface Integrals
Up: Vectors and Vector Fields
Previous: Line Integrals
Richard Fitzpatrick
2016-03-31
![]() . Let
. Let
![]() be the
vector element of line length. Vector line integrals often arise as
be the
vector element of line length. Vector line integrals often arise as
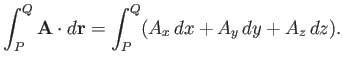
![]() . The
element of work done is
. The
element of work done is
![]() .
Take
.
Take
![]() and
and ![]() . The first route considered is along the
. The first route considered is along the ![]() -axis, so
-axis, so
![$\displaystyle W = \int_{\infty}^a \left(-\frac{1}{x^{\,2}}\right)\,dx = \left[\frac{1}{x}\right]_{\infty}^a =\frac{1}{a}.$](img6481.png)
![$\displaystyle W = \int_{\infty}^0 \frac{-y\,dy}{(a^{\,2} + y^{\,2})^{3/2}} = \left[\frac{1}{(y^{\,2}+a^{\,2})^{1/2}} \right]^0_\infty = \frac{1}{a}.$](img6482.png)