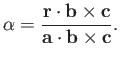Next: Vector Triple Product
Up: Vectors and Vector Fields
Previous: Rotation
Scalar Triple Product
Consider three vectors  ,
,  , and
, and 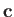 . The scalar triple product is
defined
. The scalar triple product is
defined
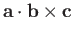 . Now,
. Now,
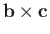 is the vector area of
the parallelogram defined by
is the vector area of
the parallelogram defined by  and
and 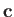 . So,
. So,
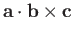 is the scalar area of this parallelogram multiplied by the component of
is the scalar area of this parallelogram multiplied by the component of  in the direction
of its normal. It follows that
in the direction
of its normal. It follows that
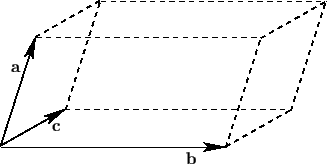
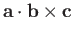 is
the volume of the parallelepiped defined by vectors
is
the volume of the parallelepiped defined by vectors  ,
,  , and
, and 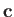 . (See Figure A.12.)
This volume is independent of how the triple product is formed from
. (See Figure A.12.)
This volume is independent of how the triple product is formed from  ,
,  ,
and
,
and 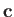 , except that
, except that
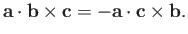 |
(A.53) |
So, the ``volume'' is positive if  ,
,  , and
, and 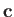 form a right-handed set
(i.e., if
form a right-handed set
(i.e., if  lies above the plane of
lies above the plane of  and
and 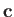 ,
in the sense determined from a right-hand circulation rule by rotating
,
in the sense determined from a right-hand circulation rule by rotating
 onto
onto 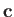 ), and negative if they form a left-handed set.
The triple product is unchanged if the dot and cross product operators are interchanged,
), and negative if they form a left-handed set.
The triple product is unchanged if the dot and cross product operators are interchanged,
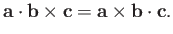 |
(A.54) |
The triple product is also invariant under any cyclic permutation of  ,
,  ,
and
,
and 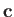 ,
,
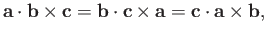 |
(A.55) |
but any anti-cyclic permutation causes it to change sign,
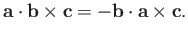 |
(A.56) |
The scalar triple product is zero if any
two of  ,
,  , and
, and 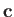 are parallel, or if
are parallel, or if  ,
,  , and
, and 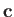 are coplanar.
are coplanar.
Figure A.12:
A vector parallelepiped.
 |
If  ,
,  , and
, and 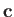 are non-coplanar then any vector
are non-coplanar then any vector  can be
written in terms of them: that is,
can be
written in terms of them: that is,
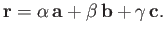 |
(A.57) |
Forming the dot product of this equation with
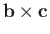 , we then obtain
, we then obtain
 |
(A.58) |
so
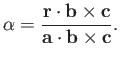 |
(A.59) |
Analogous expressions can be written for 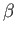 and
and 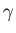 . The parameters
. The parameters  ,
, 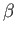 ,
and
,
and 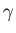 are uniquely determined provided
are uniquely determined provided
 :
that is, provided the three vectors are non-coplanar.
:
that is, provided the three vectors are non-coplanar.



Next: Vector Triple Product
Up: Vectors and Vector Fields
Previous: Rotation
Richard Fitzpatrick
2016-03-31
![]() ,
, ![]() , and
, and ![]() are non-coplanar then any vector
are non-coplanar then any vector ![]() can be
written in terms of them: that is,
can be
written in terms of them: that is,