


Next: Three-Dimensional Airfoils
Up: Incompressible Aerodynamics
Previous: Vortex Sheets
A vortex filament is necessarily associated with fluid flow circulating about the filament. Let us determine the relationship
between the filament vorticity and the flow field that it induces. This problem is mathematically identical
to determining the magnetic field generated by a current filament. In the latter case, the Maxwell equation
 |
(9.57) |
can be inverted to give the well-known Biot-Savart law (Fitzpatrick 2008)
 |
(9.58) |
Here,  is the current density, and
is the current density, and 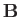 the magnetic field-strength. By analogy, given that vorticity is related to fluid
velocity via the familiar relation
the magnetic field-strength. By analogy, given that vorticity is related to fluid
velocity via the familiar relation
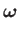 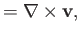 |
(9.59) |
we can write
 |
(9.60) |
This expression allows us to determine the flow field induced by a given vorticity distribution. In particular, for a vortex
filament of intensity
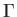 the previous expression reduces to
the previous expression reduces to
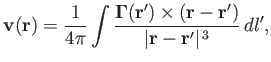 |
(9.61) |
where 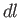 is an element of length along the filament. Likewise, for a vortex sheet of intensity per unit length
is an element of length along the filament. Likewise, for a vortex sheet of intensity per unit length
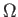 , we obtain
, we obtain
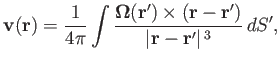 |
(9.62) |
where 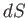 is an element of area of the sheet.
is an element of area of the sheet.



Next: Three-Dimensional Airfoils
Up: Incompressible Aerodynamics
Previous: Vortex Sheets
Richard Fitzpatrick
2016-03-31

