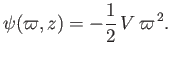Next: Point Sources
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Axisymmetric Irrotational Flow in
Uniform Flow
Consider a uniform steady stream of velocity
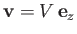 . Consider the flux (in the minus
. Consider the flux (in the minus 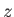 -direction) across a plane
circle of radius
-direction) across a plane
circle of radius 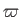 that lies in the
that lies in the  -
- plane, and whose center coincides with the
plane, and whose center coincides with the  -axis.
From the definition of the Stokes stream function (see Section 7.3), we
have
-axis.
From the definition of the Stokes stream function (see Section 7.3), we
have
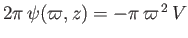 , or
, or
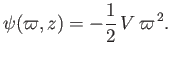 |
(7.25) |
When expressed in terms of spherical coordinates, the previous expression yields
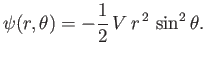 |
(7.26) |
Of course, uniform flow is irrotational [this is clear from a comparison of Equations (7.10) and (7.25)], so we can also represent the flow pattern in terms of a velocity potential: that is (see Section 5.4),
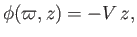 |
(7.27) |
or
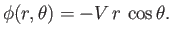 |
(7.28) |
It follows, from the previous analysis, that the velocity field of a uniform stream, running parallel to the 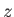 -axis,
can either be written
-axis,
can either be written
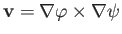 , with
, with 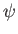 specified by Equations (7.25)-(7.26), or
specified by Equations (7.25)-(7.26), or
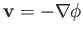 , with
, with 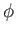 specified by Equations (7.27)-(7.28).
specified by Equations (7.27)-(7.28).



Next: Point Sources
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Axisymmetric Irrotational Flow in
Richard Fitzpatrick
2016-01-22