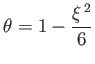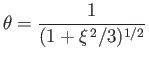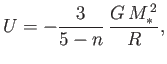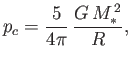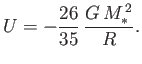Next: One-Dimensional Compressible Inviscid Flow
Up: Equilibrium of Compressible Fluids
Previous: Eddington Solar Model
- Prove that the fraction of the whole mass of an isothermal atmosphere that lies between the ground and
a horizontal plane of height
 is
is
Evaluate this fraction for 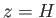 ,
, 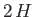 ,
, 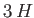 , respectively.
, respectively.
- If the absolute temperature in the atmosphere diminishes upwards according to the law
where 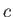 is a constant,
show that the pressure varies as
is a constant,
show that the pressure varies as
- If the absolute temperature in the atmosphere diminishes upward according to the law
where 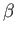 is a constant,
show that the pressure varies as
is a constant,
show that the pressure varies as
- Show that if the absolute temperature,
 , in the atmosphere is any given function
of the altitude,
, in the atmosphere is any given function
of the altitude,  , then the vertical distribution of pressure in the atmosphere is given
by
, then the vertical distribution of pressure in the atmosphere is given
by
- Show that if the Earth were surrounded by an atmosphere of uniform temperature then the
pressure a distance
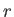 from the Earth's center would be
from the Earth's center would be
where 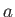 is the Earth's radius.
is the Earth's radius.
- Show that if the whole of space were occupied by air at the uniform temperature
 then the densities at the surfaces of
the various planets would be proportional to the corresponding values of
then the densities at the surfaces of
the various planets would be proportional to the corresponding values of
where 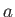 is the radius of the planet, and
is the radius of the planet, and 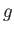 its surface gravitational acceleration.
its surface gravitational acceleration.
- Prove that in an atmosphere arranged in horizontal strata the work (per unit mass)
required to interchange two thin strata of equal mass without disturbance of the remaining
strata is
where the suffixes refer to the initial states of the two strata. Hence, show that for stability the ratio
 must increase upwards.
must increase upwards.
- A spherically symmetric star is such that
 is the mass contained within radius
is the mass contained within radius 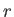 . Show that the
star's total gravitational potential energy can be written in the following three alternative forms:
. Show that the
star's total gravitational potential energy can be written in the following three alternative forms:
Here,  is the total mass,
is the total mass, 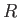 the radius,
the radius,
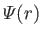 the gravitational potential per unit mass (defined such that
the gravitational potential per unit mass (defined such that
 as
as
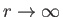 ),
),  the pressure, and
the pressure, and
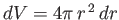 .
.
- Suppose that the pressure and density inside a spherically symmetric star are related according to the
polytropic gas law,
where 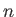 is termed the polytropic index. Let
is termed the polytropic index. Let
 , where
, where 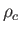 is the central
mass density. Demonstrate that
is the central
mass density. Demonstrate that 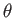 satisfies the Lane-Emden equation
satisfies the Lane-Emden equation
where  , and
, and
Show that the physical solution to the Lane-Emden equation, which is such that
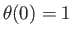 and
and
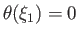 , for some
, for some 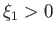 , is
, is
for  ,
,
for  , and
, and
for  . Determine the ratio of the central density to the mean density in all three cases.
Finally, demonstrate that, in the general case, the total gravitational potential energy
can be written
. Determine the ratio of the central density to the mean density in all three cases.
Finally, demonstrate that, in the general case, the total gravitational potential energy
can be written
where 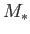 is the total mass, and
is the total mass, and
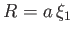 the radius.
the radius.
- A spherically symmetric star of radius
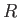 has a mass density of the form
has a mass density of the form
Show that the central mass density is four times the mean density. Demonstrate that the central
pressure is
where 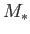 is the mass of the star. Finally, show that the total gravitational potential energy of the
star can be written
is the mass of the star. Finally, show that the total gravitational potential energy of the
star can be written



Next: One-Dimensional Compressible Inviscid Flow
Up: Equilibrium of Compressible Fluids
Previous: Eddington Solar Model
Richard Fitzpatrick
2016-01-22

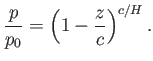
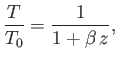
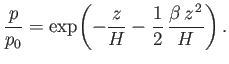
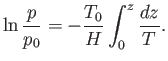
![$\displaystyle \frac{p}{p_0} = \exp\left[\frac{a^{\,2}}{H}\left(\frac{1}{r}-\frac{1}{a}\right)\right],
$](img5261.png)
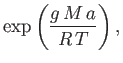
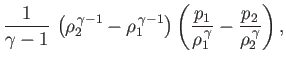

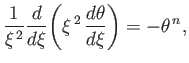
![$\displaystyle \xi=\left[\frac{(n+1)\,K}{4\pi\,G}\,\rho_c^{\,(n-1)/n}\right]^{1/2}.
$](img5272.png)