


Next: Isothermal Atmosphere
Up: Equilibrium of Compressible Fluids
Previous: Equilibrium of Compressible Fluids
In this chapter, we investigate the equilibria of compressible fluids, such as
gases. As is the case for an incompressible fluid (see Chapter 2), a compressible fluid in mechanical equilibrium must satisfy the force balance
equation
 |
(13.1) |
where 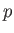 is the static fluid pressure,
is the static fluid pressure,  the mass density, and
the mass density, and
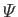 the gravitational potential energy per
unit mass.
In an ideal gas, the relationship between
the gravitational potential energy per
unit mass.
In an ideal gas, the relationship between 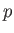 and
and  is determined by the energy conservation equation, (1.89), which
can be written
is determined by the energy conservation equation, (1.89), which
can be written
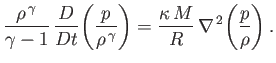 |
(13.2) |
Here, 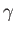 is the ratio of specific heats,
is the ratio of specific heats, 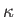 the thermal
conductivity,
the thermal
conductivity, 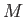 the molar mass, and
the molar mass, and 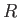 the molar ideal gas constant. Note that the viscous
heat generation term has been omitted from the previous equation (because it is zero in a stationary gas).
The limits in which the left- and right-hand sides of Equation (13.2) are dominant are termed the adiabatic and isothermal
limits, respectively.
In the isothermal limit, in which thermal transport is comparatively large, so that Equation (13.2) can only be satisfied when
the molar ideal gas constant. Note that the viscous
heat generation term has been omitted from the previous equation (because it is zero in a stationary gas).
The limits in which the left- and right-hand sides of Equation (13.2) are dominant are termed the adiabatic and isothermal
limits, respectively.
In the isothermal limit, in which thermal transport is comparatively large, so that Equation (13.2) can only be satisfied when
 , the temperature (recall that
, the temperature (recall that
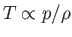 in an ideal gas) distribution in the gas becomes uniform, and the pressure and
density are consequently related according to the isothermal gas law,
in an ideal gas) distribution in the gas becomes uniform, and the pressure and
density are consequently related according to the isothermal gas law,
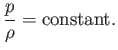 |
(13.3) |
On the other hand, in the adiabatic limit, in which thermal transport is negligible, so that Equation (13.2) can only be satisfied when
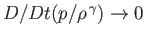 ,
the pressure and
density are related according to the adiabatic gas law,
,
the pressure and
density are related according to the adiabatic gas law,
 |
(13.4) |



Next: Isothermal Atmosphere
Up: Equilibrium of Compressible Fluids
Previous: Equilibrium of Compressible Fluids
Richard Fitzpatrick
2016-01-22