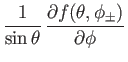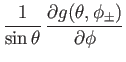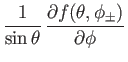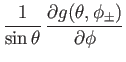

Next: Basis Eigenfunctions
Up: Terrestrial Ocean Tides
Previous: Transformation of Laplace Tidal
Another Useful Lemma
Suppose that
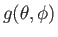 and
and
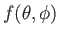 are two well-behaved functions that satisfy either
are two well-behaved functions that satisfy either
or
It is easily demonstrated that
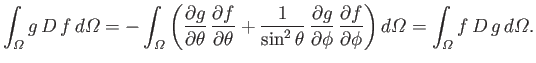 |
(12.229) |
Richard Fitzpatrick
2016-01-22